题目内容
【题目】已知抛物线y＝(m－1)x2＋m2－2m－2的图象开口向下，且经过点(0，1)．
(1)求m的值；
(2)求此抛物线的顶点坐标及对称轴；
(3)当x为何值时，y随x的增大而增大？
【答案】(1) m＝－1；(2) (3) 见解析
【解析】试题分析：开口向下说明m-1<0，将（0,1）代入函数表达式可求出m的值；函数表达式为y＝－2x2＋1，可求得对称轴是y轴，顶点坐标是（0,1）；开口向下，对称轴是y轴，所以在y轴左侧，y随x的增大而增大。
解：(1)由题意，得
，
解得m＝－1.
(2)当m＝－1时，抛物线的表达式为y＝－2x2＋1，其顶点坐标为(0，1)，对称轴为y轴．
(3)因为抛物线y＝－2x2＋1的开口向下，所以在对称轴的左侧，即当x<0时，y随x的增大而增大．
练习册系列答案
相关题目
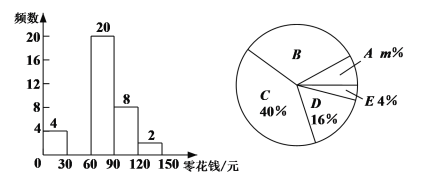
【题目】某学校为了解学生的课外阅读情况，随机抽取了50名学生，并统计他们平均每天的课外阅读时间t（单位：min），然后利用所得数据绘制成如下不完整的统计表．
课外阅读时间t | 频数 | 百分比 |
10≤t＜30 | 4 | 8% |
30≤t＜50 | 8 | 16% |
50≤t＜70 | a | 40% |
70≤t＜90 | 16 | b |
90≤t＜110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题：
（1）a= ，b= ；
（2）将频数分布直方图补充完整；
（3）若全校有900名学生，估计该校有多少学生平均每天的课外阅读时间不少于50min？
