题目内容
【题目】先列表，然后在同一平面直角坐标系内分别描点画出下列二次函数的图象，并写出对称轴与顶点坐标．
①y＝－
(x＋2)2；②y＝－
(x－1)2.
【答案】见解析
【解析】试题分析：描点画二次函数图像时，取对称轴两侧的点更容易确定函数图像，根据图像确定：抛物线y＝－
(x＋2)2的对称轴为直线x＝－2，顶点坐标为(－2，0)；
抛物线y＝－
(x－1)2的对称轴为直线x＝1，顶点坐标为(1，0)．
解：列表：
x | … | －4 | －3 | －2 | －1 | 0 | … | ||||
y＝－ | … | －1 | －0.25 | 0 | －0.25 | －1 | … | ||||
x | … | －1 | 0 | 1 | 2 | 3 | … | ||||
y＝－ | … | －1 | －0.25 | 0 | －0.25 | －1 | … | ||||
描点，连线，如图．
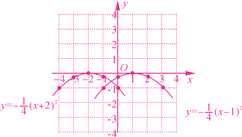
抛物线y＝－
(x＋2)2的对称轴为直线x＝－2，顶点坐标为(－2，0)；
抛物线y＝－
(x－1)2的对称轴为直线x＝1，顶点坐标为(1，0)．
练习册系列答案
相关题目
