题目内容
【题目】如果二次函数的二次项系数为1,那么此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[-2,1],求此函数图象的顶点坐标;
(2)探究下列问题:
①若一个函数的特征数为[4,-1],将此函数的图象先向右平移1个单位长度,再向上平移1个单位长度,求得到的图象对应的函数的特征数;
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
【答案】(1) (1,0);(2) ① [2,-3],②见解析
【解析】试题分析:首先根据函数的特征数可以确定函数表达式为y=x2-2x+1=(x-1)2,所以可得出顶点坐标为:(1,0);先根据函数的特征数写出函数的表达式,将表达式写成顶点式,然后再平移,平移时规律为左加右减,上加下减。求出平移后的函数表达式是顶点式,将顶点式化成y=x2+px+q的形式,即可求得特征数;如果已知两个函数的特征数,要想知道两个函数怎么平移得到的,需先将两个函数都转化成顶点式,再根据两个函数顶点式判断平移方法。
解:(1)由题意,得y=x2-2x+1=(x-1)2.
∴特征数为[-2,1]的函数图象的顶点坐标为(1,0).
(2)①特征数为[4,-1]的函数表达式为y=x2+4x-1
即y=(x+2)2-5.
∵函数图象先向右平移1个单位长度,再向上平移1个单位长度,
∴y=(x+2-1)2-5+1,即y=x2+2x-3.
∴特征数为[2,-3].
②特征数为[2,3]的函数表达式为y=x2+2x+3,即y=(x+1)2+2,
特征数为[3,4]的函数表达式为y=x2+3x+4,即
y=(x+![]() )2+
)2+![]() ,
,
∴所求平移为:先向左平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度(或先向下平移
个单位长度(或先向下平移![]() 个单位长度,再向左平移
个单位长度,再向左平移![]() 个单位长度).
个单位长度).

 教材全解字词句篇系列答案
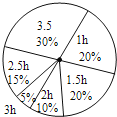
教材全解字词句篇系列答案【题目】初三年级学习压力大,放学后在家自学时间较初一、初二长,为了解学生学习时间,该年级随机抽取25%的学生问卷调查,制成统计表和扇形统计图,请你根据图表中提供的信息回答下列问题:
学习时间(h) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
人数 | 72 | 36 | 54 | 18 |
(1)初三年级共有学生_____人.
(2)在表格中的空格处填上相应的数字.
(3)表格中所提供的学生学习时间的中位数是_____,众数是_____.