题目内容
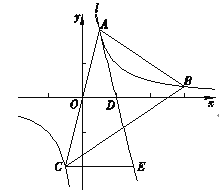
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在坐标轴上,两点的坐标分别是点
在坐标轴上,两点的坐标分别是点![]() 点
点![]() 且
且![]() 满足:
满足:![]()
![]() 边
边![]() 与
与![]() 轴交于点
轴交于点![]() 点
点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,分别与
,分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() 点
点![]() 且
且![]() .
.
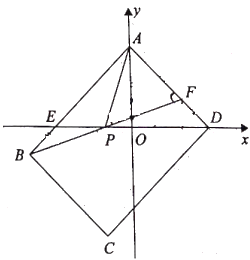
(1)求![]() 的值;
的值;
(2)若![]() 求证:
求证:![]() ;
;
(3)若点![]() 的纵坐标为
的纵坐标为![]() 则线段HF的长为 .(用含
则线段HF的长为 .(用含![]() 的代数式表示)
的代数式表示)
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)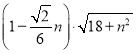 .
.
【解析】
(1)根据二次根式有意义被开方数非负和算术平方根的非负性列出两个不等式,求公共解即可求出m的值;
(2)作![]() 轴,
轴,![]() 轴,证明
轴,证明![]() 可得BP=PF,再根据直角三角形斜边上的中线等于斜边的一半可得
可得BP=PF,再根据直角三角形斜边上的中线等于斜边的一半可得![]() ,然后结合等腰三角形的性质,利用三角形的内角和定理分别求出
,然后结合等腰三角形的性质,利用三角形的内角和定理分别求出![]() 和
和![]() ,可得它们相等;
,可得它们相等;
(3)分别表示AF和AB,利用勾股定理求得BF的长,即可求得PF的长,再表示ON和PN的长度,利用平行线分线段成比例即可求得HF.
(1)∵![]()
![]() ,
,
∴![]() ,且
,且 ![]() ,
,
![]() ;
;
![]() 作
作![]() 轴,
轴,![]() 轴
轴
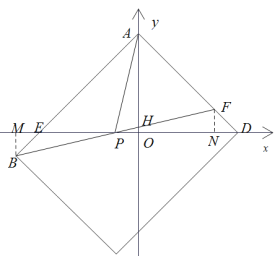
![]() ,
,
![]() ,
,
∵四边形![]() 为矩形,
为矩形,
∴∠EAD=90°,
∴![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() 轴,
轴,![]() 轴
轴
![]() ,
,
在![]() 和
和![]() 中
中
∵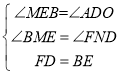 ,
,
∴![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
∵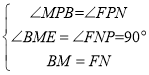
∴![]() ,
,
![]() ,
,![]() ,
,
∵![]() 中,
中,![]() ,
,
![]()
![]() ,
,![]() ,
,
∴![]() ;
;
(3)∵F点的纵坐标为n,
由(2)可知FN=ND=ME=BM=n,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
在Rt△ABF中,根据勾股定理、
![]() ,
,
∴![]() ,
,
∵FN⊥x轴,
∴FN∥OH,
∴![]() ,即
,即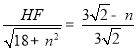 ,
,
解得:![]() ,
,
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
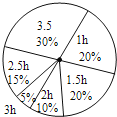
【题目】初三年级学习压力大,放学后在家自学时间较初一、初二长,为了解学生学习时间,该年级随机抽取25%的学生问卷调查,制成统计表和扇形统计图,请你根据图表中提供的信息回答下列问题:
学习时间(h) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
人数 | 72 | 36 | 54 | 18 |
(1)初三年级共有学生_____人.
(2)在表格中的空格处填上相应的数字.
(3)表格中所提供的学生学习时间的中位数是_____,众数是_____.