题目内容
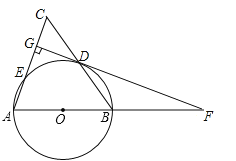
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AC平分∠DAB,直线DC与AB的延长线相交于点P,AD与PC延长线垂直,垂足为D,CE平分∠ACB,交⊙O于E.
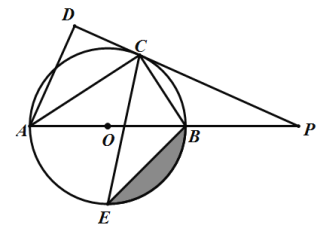
(1)求证:PC与⊙O相切;
(2)若AC=6,tan∠BEC=![]() ,求BE的长度以及图中阴影部分面积.
,求BE的长度以及图中阴影部分面积.
【答案】(1)见解析;(2)BE=![]() ,
,![]() .
.
【解析】
(1)连接OC,根据角平分线的定义、等腰三角形的性质得到∠ACO =∠DAC,得到OC∥AD,根据平行线的性质得到OC⊥PC,根据切线的判定定理证明结论;
(2)连接OE,根据角平分线的定义、圆周角定理得![]() ,证得
,证得![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,根据正切的定义求出BC,根据勾股定理求出AB,即可求出OB、BE;利用阴影部分面积=S扇形BOE
,根据正切的定义求出BC,根据勾股定理求出AB,即可求出OB、BE;利用阴影部分面积=S扇形BOE![]() 列式计算即可.
列式计算即可.
(1)如图,连结OC,
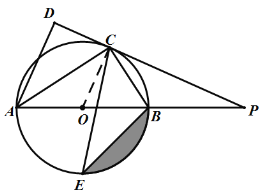
∵AC平分∠DAB,
∴∠DAC=∠CAO,
∵OC =OA,
∴∠ACO=∠CAO,
∴∠ACO =∠DAC,
∴OC∥AD,
∵AD⊥PD,则∠D=90°,
∴∠OCP=∠D=90°,
∴OC⊥PC,即PC与⊙O相切;
(2)如图,连结OE,
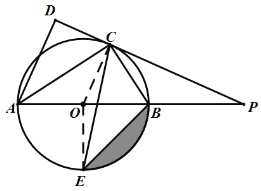
∵AB是⊙O的直径,
∴∠ACB=90°,
∵CE平分∠ACB,
∴∠BCE=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形,则
为等腰直角三角形,则![]() ,
,
∵![]() ,
,
∴∠CAB=∠BEC,
∵tan∠BEC=![]() ,
,
∴tan∠CAB = tan∠BEC=![]() ,
,
在![]() 中,AC=6,
中,AC=6,
∴![]() ,即
,即![]() ,
,
解得:BC=4,由勾股定理得AB=![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴阴影部分面积=S扇形BOE![]()
![]()
![]()
![]() .
.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目