Question

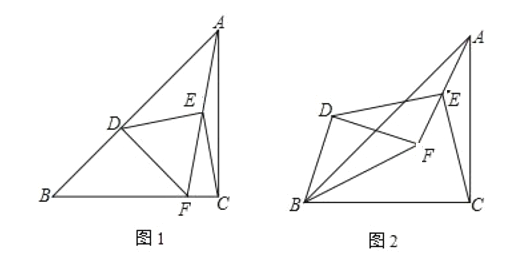
【题目】已知如图1，在中，，，点在上，交于，点是的中点．

（1）写出线段与线段的关系并证明；

（2）如图2，将绕点逆时针旋转，其它条件不变，线段与线段的关系是否变化，写出你的结论并证明；

（3）将绕点逆时针旋转一周，如果，，直接写出线段的范围．

　　　　

Answer 1

【答案】（1），，证明见解析；（2）结论不变，理由见解析；（3）最大值 最小值．

【解析】

（1）在Rt△ADF中，可得DE=AE=EF，在Rt△ABF中，可得BE=EF=EA，得证ED=EB；然后利用等腰三角形的性质以及四边形ADFB的内角和为180°，可推导得出∠DEB=90°；

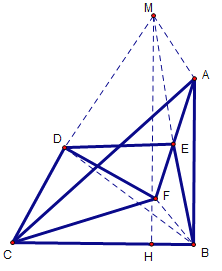
（2）如下图，先证四边形MFBA是平行四边形，再证△DCB≌△DFM，从而推导出△DMB是等腰直角三角形，最后得出结论；

（3）如下图，当点F在AC上时，CE有最大值；当点F在AC延长线上时，CE有最小值．

（1）∵DF⊥AC，点E是AF的中点

∴DE=AE=EF，∠EDF=∠DFE

∵∠ABC=90°，点E是AF的中点

∴BE=AE=EF，∠EFB=∠EBF

∴DE=EB

∵AB=BC，

∴∠DAB=45°

∴在四边形ABFD中，∠DFB=360°－90°－45°－90°=135°

∠DEB=∠DEF+∠FEB=180°－2∠EFD+180°－2∠EFB=360°－2(∠EFD+∠EFB)

=360°－2×135°=90°

∴DE⊥EB

（2）如下图，延长BE至点M处，使得ME=EB，连接MA、ME、MF、MD、FB、DB，延长MF交CB于点H

∵ME=EB，点E是AF的中点

∴四边形MFBA是平行四边形

∴MF∥AB，MF=AB

∴∠MHB=180°－∠ABC=90°

∵∠DCA=∠FCB=

∴∠DCB=45°+，∠CFH=90°－

∵∠DCF=45°，∠CDF=90°

∴∠DFC=45°，△DCF是等腰直角三角形

∴∠DFM=180°－∠DFC－∠CFH=45°+

∴∠DCB=∠DFM

∵△ABC和△CDF都是等腰直角三角形

∴DC=DF，BC=AB=MF

∴△DCB≌△DFM(SAS)

∴∠MDF=∠BDC，DB=DM

∴∠MDF+∠FDB=∠BDC+∠FDB=90°

∴△DMB是等腰直角三角形

∵点E是MB的中点

∴DE=EB，DE⊥EB

（3）当点F在AC上时，CF有最大值，图形如下：

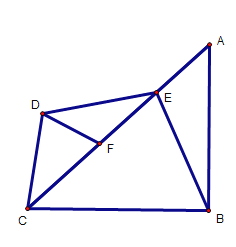
∵BC=6，∴在等腰直角△ABC中，AC=6

∵CF=3，∴AF=3

∴CE=CF+FE=CF+

当点F在AC延长线上时，CE有最小值，图形如下：

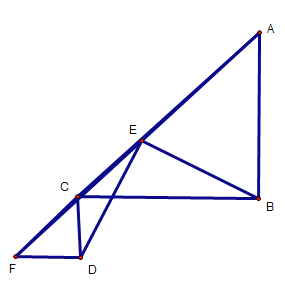
同理，CE=EF－CF