题目内容
【题目】阅读材料:
材料一:对实数a、b,定义![]() 的含义为:当
的含义为:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .例如:
.例如:![]() ;
;![]() .
.
材料二:关于数学家高斯的故事,200多年前,高斯的算术老师提出了下面的问:![]() 据说,当其他同学忙于把100个数逐项相加时,十岁的高斯却用下面的方法迅速算出了正确答案:
据说,当其他同学忙于把100个数逐项相加时,十岁的高斯却用下面的方法迅速算出了正确答案:![]() .也可以这样理解:令
.也可以这样理解:令![]() ①,则
①,则![]() ②,①+②:
②,①+②:![]() ,即
,即![]() .
.
根据以上材料,回答下列问题:
(1)已知![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,且
,且![]() ,化简:
,化简:![]() ;
;
(3)对于正数m,有![]() ,求
,求![]() …+
…+![]() 的值.
的值.
【答案】(1)-12
(2)3
(3)19800
【解析】
(1)根据![]() ,且
,且![]() ,可求得x、y的取值范围代入公式可求
,可求得x、y的取值范围代入公式可求![]() 的值;
的值;
(2)根据![]() ,确定2x和3的大小关系,1和x的大小关系,代入不等式求解x的解集,再化简求解.
,确定2x和3的大小关系,1和x的大小关系,代入不等式求解x的解集,再化简求解.
(3)根据正数m,有![]() ,可求出m的值,再代入
,可求出m的值,再代入![]() ,利用
,利用![]() ,可求解.
,可求解.
(1)∵![]() ,且
,且![]()
可得![]() ,
,
原式=![]()
(2)![]() 可得
可得![]()
![]()
得![]()
所以![]()
![]()
(3)![]()
∵![]()
∴![]()
∴![]()
∴![]()
m为正数,所以m=1
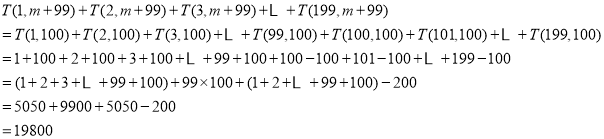

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)中的x与y的部分对应值如表所示,则下列结论中,正确的个数有( )
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
①a<0;②当x<0时,y<3;③当x>1时,y的值随x值的增大而减小;④方程ax2+bx+c=5有两个不相等的实数根.
A.4个B.3个C.2个D.1个