ЬтФПФкШн
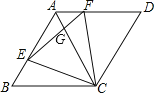
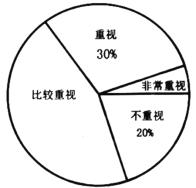
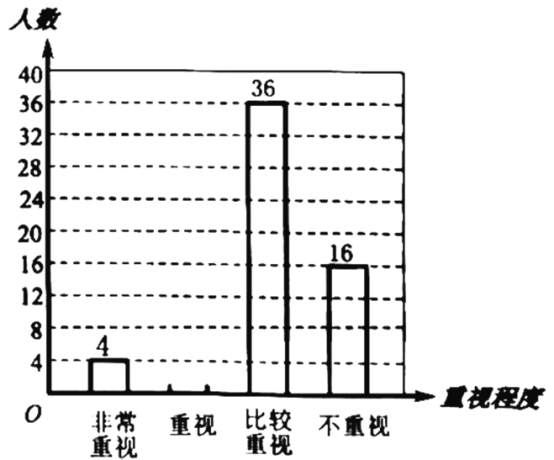
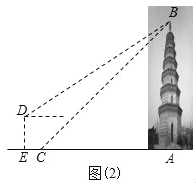
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌдкдЅЮїФЯЕЫжнЪаДѓЪЎзжНжЮїФЯЗНЃЌЫЪСЂзХвЛзљЙХРЯНЈжў-ИЃЪЄЫТшѓЫўЃЌНЈгкББЫЮЬьЪЅЪЎФъЃЈЙЋдЊ1032ФъЃЉЃЌбЇЭъСЫШ§НЧКЏЪ§жЊЪЖКѓЃЌФГаЃЁАЪ§бЇЩчЭХЁБЕФСѕУїКЭЭѕЛЊОіЖЈгУздМКбЇЕНЕФжЊЪЖВтСПЁАИЃЪЄЫТшѓЫўЁБЕФИпЖШЃЎШчЭМЃЈ2ЃЉЃЌСѕУїдкЕуCДІВтЕУЫўЖЅBЕФбіНЧЮЊ45ЁуЃЌЭѕЛЊдкИпЬЈЩЯЕФЕуDДІВтЕУЫўЖЅBЕФбіНЧЮЊ40ЁуЃЌШєИпЬЈDEИпЮЊ5УзЃЌЕуDЕНЕуCЕФЫЎЦНОрРыECЮЊ1.3УзЃЌЧвAЁЂCЁЂEШ§ЕуЙВЯпЃЌЧѓИУЫўABЕФИпЖШЃЎЃЈВЮПМЪ§ОнЃКsin40ЁуЁж0.64ЃЌcos40ЁуЁж0.77ЃЌtan40ЁуЁж0.84ЃЌНсЙћБЃСєећЪ§ЃЉ

ЁОД№АИЁП38Уз
ЁОНтЮіЁП
зїDMЁЭABгкMЃЌНЛCBгкFЃЌCGЁЭDMгкGЃЌИљОнОиаЮЕФаджЪЕУЕНCG=DE=5ЃЌDG=EC=1.3ЃЌЩшFM=xУзЃЌИљОне§ЧаЕФЖЈвхгУxБэЪОГіDMЁЂBMЃЌНсКЯЭМаЮСаГіЗНГЬЃЌНтЗНГЬЕУЕНД№АИЃЎ
НтЃКШчЭМЃЌзїDMЁЭABгкMЃЌНЛCBгкFЃЌCGЁЭDMгкGЃЌдђЫФБпаЮDECGЮЊОиаЮЃЌ
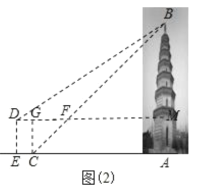
ЁрCGЃНDEЃН5ЃЌDGЃНECЃН1.3ЃЌ
ЩшFMЃНxУзЃЌгЩЬтвтЕУЃЌЁЯBDMЃН40ЁуЃЌЁЯBFMЃНЁЯBCAЃН45ЁуЃЌ
ЁрЁЯCFGЃН45ЁуЃЌBMЃНFMЃНxЃЌ
ЁрGFЃНGCЃН5ЃЌ
ЁрDFЃНDG+GFЃН5+1.3ЃН6.3ЃЌ
дкRtЁїBDMжаЃЌtanЁЯBDMЃН![]() ЃЌ
ЃЌ
ЁрDMЃН![]() ЃЌ
ЃЌ
гЩЬтвтЕУЃЌDMЉDFЃНFMЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃЌxЁж33.2ЃЌдђBAЃНBM+AMЃН38.2Ёж38ЃЈУзЃЉЃЌ
Д№ЃКИУЫўABЕФИпЖШдМЮЊ38УзЃЎ

 МЄЛюЫМЮЌгХМгПЮЬУЯЕСаД№АИ
МЄЛюЫМЮЌгХМгПЮЬУЯЕСаД№АИ ЛюСІЪдОэЯЕСаД№АИ
ЛюСІЪдОэЯЕСаД№АИ ПЮПЮгХФмСІХргХ100ЗжЯЕСаД№АИ
ПЮПЮгХФмСІХргХ100ЗжЯЕСаД№АИ