题目内容
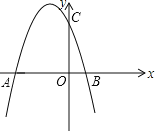
【题目】如图，抛物线y＝ax2+bx+3与x轴交于A（﹣3，0），B（l，0）两点，与y轴交于点C．
（1）求抛物线的解析式；
（2）点P是抛物线上的动点，且满足S△PAO＝2S△PCO，求出P点的坐标；
（3）连接BC，点E是x轴一动点，点F是抛物线上一动点，若以B、C、E、F为顶点的四边形是平行四边形时，请直接写出点F的坐标．
【答案】（1）y＝﹣x2﹣2x+3；（2）点P（
，﹣2）或（﹣，2）或（﹣2+
，﹣4+2）或（﹣2﹣，﹣4﹣2）；（3）点F坐标（﹣2，3）或（﹣1+，﹣3）或（﹣1﹣，﹣3）
【解析】
（1）由待定系数法可求解析式；
（2）求出点C坐标，可得OA＝OC＝3，由面积关系列出方程可求解；
（3）分两种情况讨论，利用平行四边形的性质可求解．
解：（1）∵抛物线y＝ax2+bx+3与x轴交于A（﹣3，0），B（l，0）两点，
∴
，
解得：
，
∴抛物线的解析式为：y＝﹣x2﹣2x+3；
（2）∵抛物线y＝﹣x2﹣2x+3与y轴交于点C，
∴点C（0，3）
∴OA＝OC＝3，
设点P（x，﹣x2﹣2x+3）
∵S△PAO＝2S△PCO，
∴
×3×|﹣x2﹣2x+3|＝2××3×|x|，
∴x＝±或x＝﹣2±，
∴点P（，﹣2）或（﹣，2）或（﹣2+，﹣4+2）或（﹣2﹣，﹣4﹣2）；
（3）若BC为边，且四边形BCFE是平行四边形，
∴CF∥BE，
∴点F与点C纵坐标相等，
∴3＝﹣x2﹣2x+3，
∴x1＝﹣2，x2＝0，
∴点F（﹣2，3）
若BC为边，且四边形BCEF是平行四边形，
∴BE与CF互相平分，
∵BE中点纵坐标为0，且点C纵坐标为3，
∴点F的纵坐标为﹣3，
∴﹣3＝﹣x2﹣2x+3
∴x＝﹣1±，
∴点F（﹣1+，﹣3）或（﹣1﹣，﹣3）；
若BC为对角线，则四边形BECF是平行四边形，
∴BC与EF互相平分，
∵BC中点纵坐标为
，且点E的纵坐标为0，
∴点F的纵坐标为3，
∴点F（﹣2，3），
综上所述，点F坐标（﹣2，3）或（﹣1+，﹣3）或（﹣1﹣，﹣3）．
