Question

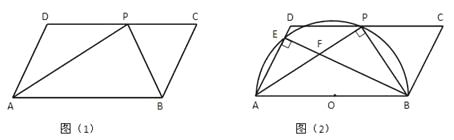
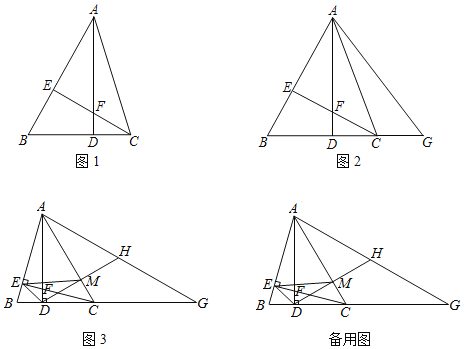
【题目】如图1，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，∠ACE＝45°．

(1)求证：BE＝EF；

(2)如图2，G在BC的延长线上，连接GA，若GA＝GB，求证：AC平分∠DAG；

(3)如图3，在(2)的条件下，H为AG的中点，连接DH交AC于M，连接EM、ED，若S△EMC＝4，∠BAD＝15°，求AM的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）AM＝6．

【解析】

(1)先判断出AE＝CE，再利用等角的余角相等判断出∠EAF＝∠ECB，进而判断出△AEF≌△CEB，即可得出结论；

(2)先利用三角形外角的性质得出∠AEF＝45°+∠CAD，进而得出∠B＝45°+∠CAD，而∠B＝∠BAG，得出∠BAG＝45°+∠CAD，而∠BAG＝45°+∠CAG，即可得出结论；

(3)先判断出△ADH是等边三角形，进而利用含30度角的直角三角形的性质判断出AM＝3CM，进而求出△ACM的面积，即可求出AE，进而求出AC，即可得出结论．

解：(1)∵CE⊥AB，

∴∠AEC＝∠BEC＝90°，

∵∠ACE＝45°，

∴∠CAE＝45°＝∠ACE，

∴AE＝CE，

∵AD⊥BC，

∴∠ADC＝90°，

∴∠ECB+∠CFD＝90°，

∵∠CFD＝∠AFE，

∴∠ECB+∠AFE＝90°，

∵∠EAF+∠AFE＝90°，

∴∠EAF＝∠ECB，

∵∠AEF＝∠CEB＝90°，

∴△AEF≌△CEB(ASA)，

∴BE＝EF；

(2)∵△AEF≌△CEB，

∴∠AFE＝∠B，

∵∠AFE＝∠ACE+∠CAD＝45°+∠CAD，

∴∠B＝45°+∠CAD，

∵AG＝BG，

∴∠B＝∠BAG，

∴∠BAG＝45°+∠CAD，

∵∠BAG＝∠CAE+∠CAG＝45°+∠CAG，

∴∠CAD＝∠CAG，

∴AC平分∠DAG；

(3)∵∠BAD＝15°，∠CAE＝45°，

∴∠CAD＝∠CAE﹣∠BAD＝30°，

∵∠CAD＝∠CAG，

∴∠DAG＝2∠CAD＝60°，

在Rt△ADG中，点H是AG的中点，

∴DH＝AH，

∴△ADH是等边三角形，

∴∠ADH＝60°，AD＝AH，

∵∠CAD＝∠CAG，

∴AC⊥DH，

即：∠AMD＝∠DMC＝90°

∵∠ADC＝90°，

∴∠CDM＝30°，

在Rt△DMC中，CD=2CM，DM＝CM，

在Rt△AMD中，AM＝DM＝×CM＝3CM，

∴S△AEM＝3S△CEM＝3×4＝12，

∴S△ACE＝S△CEM+S△AEM＝16，

∵∠AEC＝90°，AE＝CE，

∴S△ACE＝AE2＝16，

∴AE＝4，

∴AC＝AE＝8，

∴AM+CM＝8，

∵AM＝3CM，

∴3CM+CM＝8，

∴CM＝2，

∴AM＝3CM＝6．