题目内容
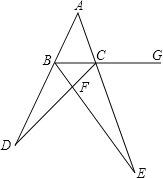
【题目】如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A, B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y (cm).

(1)填空:从图可知,每个小长方形较长的一边长是_________cm (用含y的代数式表示).
(2)分别求出阴影 A,B的面积,并计算阴影 A,B的面积差?(用含x,y的式子表示)
(3)当y=10时,阴影 A与阴影 B的面积差会随着x的变化而变化吗?请你作出判断,并说明理由.
【答案】(1)60-3y;(2)SA=60x-120y-3xy+6y2,SB=3xy+9y2-180y,SA﹣SB=60x+60y-6xy-3y2(3)不变化,为定值300
【解析】
(1)从图可知,每个小长方形较长的一边长是(60-3y)cm;
(2)阴影部分A的面积是(60-3y)(x-2y)cm2,阴影部分B的面积是3y[x-(60-3y)]cm2,所以阴影A,B的面积差是:(60-3y)(x-2y)-3y[x-(60-3y)]
(3)把(2)中阴影A,B的面积的式子相减得300 cm2,判断出不随x的变化而变化.
(1)从图可知,每个小长方形较长的一边长是(60-3y)cm;
(2)SA=(x-2y)(60-3y)=60x-120y-3xy+6y2
SB=3y [x-(60-3y)]= 3y (x+3y-60) =3xy+9y2-180y
SA﹣SB=60x-120y-3xy+6y2﹣(3xy+9y2-180y)=60x+60y-6xy-3y2
(3)当y=10时,阴影 A与阴影 B的面积SA-SB=60x+600-60x-300= 300,是定值,不会随着x的变化而变化.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目