ЬтФПФкШн
ЁОЬтФПЁПдкЛЗОГДДгХЛюЖЏжаЃЌФГОгУёаЁЧјвЊдквЛПщППЧНЃЈЧНГЄ25УзЃЉЕФПеЕиЩЯаоНЈвЛИіОиаЮбјМІГЁЃЌбјМІГЁЕФвЛБпППЧНЃЌШчЙћгУ60mГЄЕФРщАЪЮЇГЩжаМфгавЛЕРРщАЪЕФбјМІГЁЃЌЩшбјМІГЁЦНаагкЧНЕФвЛБпBCЕФГЄЮЊxЃЈmЃЉЃЌбјМІГЁЕФУцЛ§ЮЊyЃЈm2ЃЉ
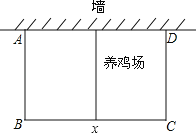
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉбјМІГЁЕФУцЛ§ФмДяЕН300m2Т№ЃПШєФмЃЌЧѓГіДЫЪБxЕФжЕЃЌШєВЛФмЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉИљОнЃЈ1ЃЉжаЧѓЕУЕФКЏЪ§ЙиЯЕЪНЃЌХаЖЯЕБxШЁКЮжЕЪБЃЌбјМІГЁЕФУцЛ§зюДѓЃПзюДѓУцЛ§ЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉy=x![]() ЃЈ60ЉxЃЉ=Љ
ЃЈ60ЉxЃЉ=Љ![]() x2+20xЃЈ0ЃМxЁм25ЃЉЃЛЃЈ2ЃЉВЛФмЃЌМћНтЮіЃЛЃЈ3ЃЉЕБxШЁ25mЪБЃЌбјМІГЁЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ
x2+20xЃЈ0ЃМxЁм25ЃЉЃЛЃЈ2ЃЉВЛФмЃЌМћНтЮіЃЛЃЈ3ЃЉЕБxШЁ25mЪБЃЌбјМІГЁЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ![]() m2ЃЎ
m2ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЯШгУxБэЪОГіABЃЌИљОнОиаЮЕФУцЛ§ЙЋЪНЕУЕНy=Љ![]() x2+20xЃЌШЛКѓРћгУЧНГЄ25УзПЩЕУЕНxЕФШЁжЕЗЖЮЇЃЛ
x2+20xЃЌШЛКѓРћгУЧНГЄ25УзПЩЕУЕНxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉСюy=300ЕУЕНЉ![]() x2+20x=300ЃЌНтЕУx=30ЃЌШЛКѓИљОнxЕФШЁжЕЗЖЮЇПЩХаЖЯбјМІГЁЕФУцЛ§ВЛФмДяЕН300m2ЃЛ
x2+20x=300ЃЌНтЕУx=30ЃЌШЛКѓИљОнxЕФШЁжЕЗЖЮЇПЩХаЖЯбјМІГЁЕФУцЛ§ВЛФмДяЕН300m2ЃЛ
ЃЈ3ЃЉАбЃЈ1ЃЉжаЕФНтЮіЪНХфГЩЖЅЕуЪНЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтЃЎ
НтЃКЃЈ1ЃЉBC=xЃЌдђAB=![]() ЃЈ60ЉxЃЉЃЌ
ЃЈ60ЉxЃЉЃЌ
Ыљвдy=x![]() ЃЈ60ЉxЃЉ=Љ
ЃЈ60ЉxЃЉ=Љ![]() x2+20xЃЈ0ЃМxЁм25ЃЉЃЛ
x2+20xЃЈ0ЃМxЁм25ЃЉЃЛ
ЃЈ2ЃЉВЛФмЃЎРэгЩШчЯТЃК
ЕБy=300ЪБЃЌМДЉ![]() x2+20x=300ЃЌ
x2+20x=300ЃЌ
ећРэЕУx2Љ60x+900=0ЃЌНтЕУx1=x2=30ЃЌ
вђЮЊ0ЃМxЁм25ЃЌ
Ыљвдx=30ВЛТњзуЬѕМўЃЌ
ЫљвдбјМІГЁЕФУцЛ§ФмДяЕН300m2ЃЛ
ЃЈ3ЃЉy=Љ![]() x2+20x=Љ
x2+20x=Љ![]() ЃЈxЉ30ЃЉ2+300ЃЌ
ЃЈxЉ30ЃЉ2+300ЃЌ
вђЮЊ0ЃМxЁм25ЃЌ
ЫљвдЕБx=25ЪБЃЌyЕФжЕзюДѓЃЌзюДѓжЕЮЊЉ![]() ЃЈ25Љ30ЃЉ2+300=
ЃЈ25Љ30ЃЉ2+300=![]() ЃЎ
ЃЎ
Д№ЃКЕБxШЁ25mЪБЃЌбјМІГЁЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ![]() m2ЃЎ
m2ЃЎ