题目内容
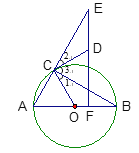
【题目】如图,AB为⊙O的直径,∠ABC=30°,ED⊥AB于点F,CD切⊙O于点C,交EF于点D.
(1)∠E= °;
(2)△DCE是什么特殊三角形?请说明理由;
(3)当⊙O的半径为1,BF=![]() 时,求证△DCE≌△OCB.
时,求证△DCE≌△OCB.

【答案】(1)30°; (2)△DCE为等腰三角形; 理由见解析;(3)证明见解析
【解析】【试题分析】(1)AB为⊙O的直径,则
![]() ,因为∠ABC=30°,则
,因为∠ABC=30°,则![]() ,因为ED⊥AB,则∠E=30°
,因为ED⊥AB,则∠E=30°
(2)△DCE为等腰三角形.理由:∠1=30°,根据同角的余角相等,得∠2=30°=∠E
得△DCE为等腰三角形.
(3)由(2)得△DCE∽△OCB,在Rt△ABC中, 求得BC=![]() =
=![]() . AF=AB-BF=2-
. AF=AB-BF=2-![]() =
=![]() ,在Rt△AEF中,
,在Rt△AEF中,
则AE=2AF=1+![]() ,CE=AE-AC=1+
,CE=AE-AC=1+![]() -1=
-1=![]() .
.
CE=BC=![]() ,△DCE≌△OCB得证。
,△DCE≌△OCB得证。
【试题解析】
(1)AB为⊙O的直径,则
![]() ,因为∠ABC=30°,则
,因为∠ABC=30°,则![]() ,因为ED⊥AB,则∠E=30°
,因为ED⊥AB,则∠E=30°
(2)△DCE为等腰三角形.
∵CD是⊙O的切线,∴∠OCD=90°.
即∠1+∠3=90°(如图).
∵AB为⊙O的直径,∴∠ACB=90°,
∴∠ECB=90°,即∠2+∠3=90°,
∴∠1=∠2.∵∠B=30°,∴∠A=60°;
∵OC=OB,∴∠1=∠B=30°,∴∠2=30°.
∵ED⊥AB于点F,∴∠E=90°-∠A=30°,
∴∠E=∠2,故△DCE的等腰三角形;
(3)证明:在Rt△ABC中,∵∠B=30°,
∴AC=![]() AB=
AB=![]() ×2=1.
×2=1.
∴BC=![]() =
=![]() .
.
AF=AB-BF=2-![]() =
=![]()
在Rt△AEF中,∵∠E=30°,
∴AE=2AF=1+![]() ,
,
∴CE=AE-AC=1+![]() -1=
-1=![]() .在△DCE和△OCB中,
.在△DCE和△OCB中,
∵∠E=∠2=∠B=∠1=30°,CE=BC=![]() ,∴△DCE≌△OCB.
,∴△DCE≌△OCB.

 名校课堂系列答案
名校课堂系列答案【题目】某校为了了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四个等级,并绘制成下面的频数分布表(表一)和扇形统计图(图①)。
表一
等级 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | 12 | 0.24 | |
B | 8分 |
|
|
7分 | 8 | 0.16 | |
C | 6分 |
|
|
5分 | 1 | 0.02 | |
D | 5分以下 | 3 | 0.06 |
合计 | 50 | 1.00 |

(1)求出![]() 、
、![]() 的值,直接写出
的值,直接写出![]() 、
、![]() 的值;
的值;
(2)求表示得分为C等级的扇形的圆心角的度数;
(3)如果该校九年级共有男生250名,试估计这250名男生中成绩达到A等级的人数约有多少人?