Question

【题目】已知抛物线与轴交于Ａ、Ｂ两点（Ａ在Ｂ的左侧），且Ａ、Ｂ两点的横坐标是方程－１２＝０的两个根．抛物线与轴的正半轴交于点Ｃ，且ＯＣ＝ＡＢ．

（１）求Ａ、Ｂ、Ｃ三点的坐标；

（２）求此抛物线的解析式；

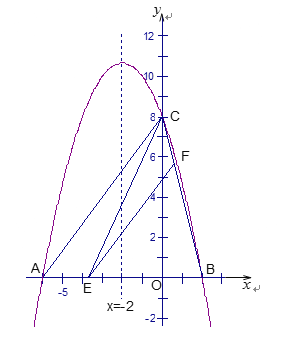
（３）连接ＡＣ、ＢＣ，若点Ｅ是线段ＡＢ上的一个动点（与点Ａ、点Ｂ不重合），过点Ｅ作ＥＦ∥ＡＣ交ＢＣ于点Ｆ，连接ＣＥ，设ＡＥ的长为，△ＣＥＦ的面积为Ｓ，求Ｓ与之间的函数关系式；

（４）对于（３），试说明Ｓ是否存在最大值或最小值，若存在，请求出此值，并求出此时点Ｅ的坐标，判断此时△ＢＣＥ的形状；若不存在，请说明理由．

Answer 1

【答案】（１）Ａ（－６，０）、Ｂ（２，０）、Ｃ（０，８）；

（２）抛物线的解析式为＝－＋８；

（３）Ｓ＝－　（０＜＜８）；

（４）存在最大值； △ＢＣＥ为等腰三角形．

【解析】【试题分析】（1）解方程－１２＝０得到＝－６， ＝２，得Ａ（－６，０）、Ｂ（２，０），根据ＯＣ＝ＡＢ，得Ｃ（０，８），即Ａ（－６，０）、Ｂ（２，０）、Ｃ（０，８）；

（2）将（1）中的三个坐标代入即可，即得解得，则所求抛物线的解析式为＝－＋８；

（3）依题意，ＡＥ＝，则ＢＥ＝８－．ＥＦ∥ＡＣ，得△ＢＥＦ∽△ＢＡＣ，

设ＢＥ边上的高为，由相似三角形的性质“对应高的比等于相似比”， 得：ＢＥ边上的高︰ＢＡ边上的高＝ＢＥ︰ＢＡ， 即︰ＯＣ＝ＢＥ︰ＢＡ，

∴︰８＝（８－）︰８，∴＝８－．如图，Ｓ＝Ｓ△ＣＥＦ＝Ｓ△ＡＢＣ－Ｓ△ＡＣＥ－Ｓ△ＢＥＦ　

＝×８×８－×８－ ＝－　（０＜＜８）；

（４）存在最大值．利用配方法求二次函数的极值，即Ｓ＝－＝－＝－＋８，得当＝４时，Ｓ有最大值８， 即ＡＥ＝４，

∴点Ｅ的坐标为Ｅ（－２，０），∵Ｂ（２，０），∴ＯＣ⊥ＥＢ且平行ＥＢ，

即ＣＥ＝ＣＢ，△ＢＣＥ为等腰三角形．

【试题解析】

（１）由方程－１２＝０

得（＋６）（－２）＝０，

∴＝－６， ＝２，

由题意得Ａ（－６，０）、Ｂ（２，０）．ＡＢ＝６－（－２）＝８，

∵ＯＣ＝ＡＢ且Ｃ点在轴的正半轴上，

∴Ｃ（０，８）．∴Ａ、Ｂ、Ｃ三点的坐标分别为：

Ａ（－６，０）、Ｂ（２，０）、Ｃ（０，８）；

（２）∵点Ｃ（０，８）在抛物线上，

当＝０时， ＝８，∴＝８．

将Ａ（－６，０）、Ｂ（２，０）代入，

得，

解得，∴所求抛物线的解析式为＝－＋８；

（３）依题意，ＡＥ＝，则ＢＥ＝８－．

∵ＥＦ∥ＡＣ，∴△ＢＥＦ∽△ＢＡＣ，

设ＢＥ边上的高为，

即︰ＯＣ＝ＢＥ︰ＢＡ，

∴︰８＝（８－）︰８，

∴＝８－．如图，

Ｓ＝Ｓ△ＣＥＦ＝Ｓ△ＡＢＣ－Ｓ△ＡＣＥ－Ｓ△ＢＥＦ　

＝×８×８－×８－ ，

化简整理得Ｓ＝－　（０＜＜８）；

（４）存在最大值．∵Ｓ＝－

＝－＝－＋８，

∵－＜０，∴当＝４时，Ｓ有最大值８，

Ｓ最大值＝８． ＝４，即ＡＥ＝４，

∴点Ｅ的坐标为Ｅ（－２，０），

∵Ｂ（２，０），∴ＯＣ⊥ＥＢ且平行ＥＢ，

即ＣＥ＝ＣＢ，

∴△ＢＣＥ为等腰三角形．