题目内容
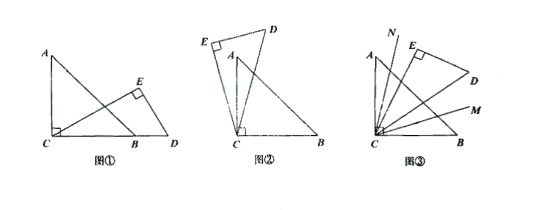
【题目】感知:如图①,在平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .过点
.过点![]() 的直线
的直线![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() .易证:
.易证:![]() (不需要证明).
(不需要证明).
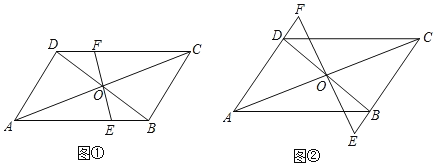
探究:若图①中的直线![]() 分别交边
分别交边![]() 、
、![]() 的延长线于点
的延长线于点![]() 、
、![]() ,其它条件不变,如图②.
,其它条件不变,如图②.
求证:![]() .
.
应用:在图②中,连结![]() .若
.若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的长是__________,四边形
的长是__________,四边形![]() 的面积是__________.
的面积是__________.
【答案】探究:证明见解析;应用:10,36
【解析】
探究:根据平行四边形的性质得到AB∥CD,OB=OD,根据AAS可证明△BOE≌△DOF.
应用:根据平行四边形的性质、梯形的面积公式计算即可.
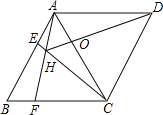
探究:如图②.
∵四边形ABCD是平行四边形,∴AD∥BC,OD=OB,∴∠ODF=∠OBE,∠E=∠F.
在△BOE和△DOF中,∵ ,∴△BOE≌△DOF(AAS).
,∴△BOE≌△DOF(AAS).
应用:
∵∠ADB=90°,AB=10,AD=6,∴BD![]() 8.
8.
∵BE=![]() BC,BC=AD=6,∴BE=3.
BC,BC=AD=6,∴BE=3.
∵AD∥BE,∴BD⊥CE.在Rt△OBE中,OB![]() BD=4,BE=3,∴OE=5,由探究得:△BOE≌△DOF,∴OE=OF=5,∴EF=10,四边形AEBD的面积
BD=4,BE=3,∴OE=5,由探究得:△BOE≌△DOF,∴OE=OF=5,∴EF=10,四边形AEBD的面积![]() 36.
36.
故答案为:10,36.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目