题目内容
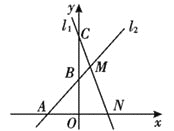
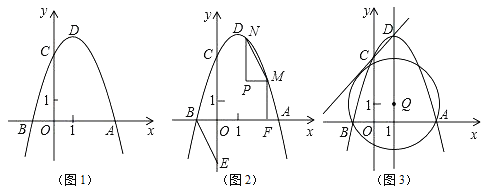
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示).
(2)若以AD为直径的圆经过点C.
①求a的值.
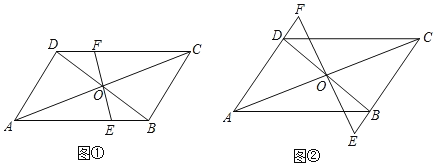
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段BF=2MF,求点M、N的坐标.
③如图3,点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,求点Q的坐标.
【答案】(1)D(1,﹣4a);(2)①a=﹣1;②M(![]() ,
, ![]() )、N(
)、N(![]() ,
, ![]() );③Q的坐标为(1,
);③Q的坐标为(1, ![]() )或(1,
)或(1, ![]() ).
).
【解析】分析: (1)将二次函数的解析式进行配方即可得到顶点D的坐标.
(2)①以AD为直径的圆经过点C,即点C在以AD为直径的圆的圆周上,依据圆周角定理不难得出△ACD是个直角三角形,且∠ACD=90°,A点坐标可得,而C、D的坐标可由a表达出来,在得出AC、CD、AD的长度表达式后,依据勾股定理列等式即可求出a的值.
②将△OBE绕平面内某一点旋转180°得到△PMN,说明了PM正好和x轴平行,且PM=OB=1,所以求M、N的坐标关键是求出点M的坐标;首先根据①的函数解析式设出M点的坐标,然后根据题干条件:BF=2MF作为等量关系进行解答即可.
③设⊙Q与直线CD的切点为G,连接QG,由C、D两点的坐标不难判断出∠CDQ=45°,那么△QGD为等腰直角三角形,即QD =2QG =2QB ,设出点Q的坐标,然后用Q点纵坐标表达出QD、QB的长,根据上面的等式列方程即可求出点Q的坐标.
详解:
(1)∵y=ax2﹣2ax﹣3a=a(x﹣1)2﹣4a,
∴D(1,﹣4a).
(2)①∵以AD为直径的圆经过点C,
∴△ACD为直角三角形,且∠ACD=90°;
由y=ax2﹣2ax﹣3a=a(x﹣3)(x+1)知,A(3,0)、B(﹣1,0)、C(0,﹣3a),则:
AC2=9a2+9、CD2=a2+1、AD2=16a2+4
由勾股定理得:AC2+CD2=AD2,即:9a2+9+a2+1=16a2+4,
化简,得:a2=1,由a<0,得:a=﹣1,
②∵a=﹣1,
∴抛物线的解析式:y=﹣x2+2x+3,D(1,4).
∵将△OBE绕平面内某一点旋转180°得到△PMN,
∴PM∥x轴,且PM=OB=1;
设M(x,﹣x2+2x+3),则OF=x,MF=﹣x2+2x+3,BF=OF+OB=x+1;
∵BF=2MF,
∴x+1=2(﹣x2+2x+3),化简,得:2x2﹣3x﹣5=0
解得:x1=﹣1(舍去)、x2=![]() .
.
∴M(![]() ,
, ![]() )、N(
)、N(![]() ,
, ![]() ).
).
③设⊙Q与直线CD的切点为G,连接QG,过C作CH⊥QD于H,如下图:
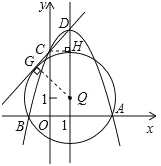
∵C(0,3)、D(1,4),
∴CH=DH=1,即△CHD是等腰直角三角形,
∴△QGD也是等腰直角三角形,即:QD2=2QG2;
设Q(1,b),则QD=4﹣b,QG2=QB2=b2+4;
得:(4﹣b)2=2(b2+4),
化简,得:b2+8b﹣8=0,解得:b=﹣4±2![]() ;
;
即点Q的坐标为(1, ![]() )或(1,
)或(1, ![]() ).
).
点睛: 此题主要考查了二次函数解析式的确定、旋转图形的性质、圆周角定理以及直线和圆的位置关系等重要知识点;后两个小题较难,最后一题中,通过构建等腰直角三角形找出QD和⊙Q半径间的数量关系是解题题目的关键.