题目内容
【题目】如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A﹣C﹣B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C﹣B﹣A向A点运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t=秒时,△PCQ的面积等于8cm2 . 
【答案】2或4或 ![]()
【解析】解:①设经过x秒,使△PCQ的面积等于8cm2,
点P在线段AC上,点Q在线段CB上(0<x≤4),
依题意有 ![]() (6﹣x)2x=8,
(6﹣x)2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意.
故经过2秒或4秒,△PBQ的面积等于8cm2;
②点P在线段AC上,点Q在线段BA上(4<m<6)如图1,

设经过m秒,使△PCQ的面积等于8cm2,
则BQ=2m﹣8,AQ=18﹣2m,
过Q作QH⊥AC于H,则QH∥BC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴QH= ![]() ,
,
∴依题意有 ![]() (6﹣m)
(6﹣m) ![]() =8,
=8,
解得:m= ![]() (不合题意);
(不合题意);
③点P在线段BC上,点Q在线段AB上(6<x<9),如图2,
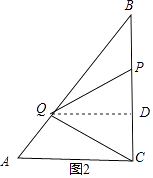
设经过n秒,使△PCQ的面积等于8cm2,
则PC=n﹣6BQ=2n﹣8,
过Q作QD⊥BC于D,则QD∥AC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴QD= ![]() ,
,
∴依题意有 ![]() (n﹣6)
(n﹣6) ![]() =8,
=8,
解得:n= ![]() ,n=
,n= ![]() (不合题意);
(不合题意);
综上所述,当t=2或4或 ![]() 秒时,△PCQ的面积等于8cm2.
秒时,△PCQ的面积等于8cm2.
所以答案是:2或4或 ![]() .
.
【考点精析】通过灵活运用平行线分线段成比例,掌握三条平行线截两条直线,所得的对应线段成比例即可以解答此题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目