Question

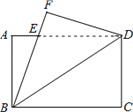
【题目】如图是明明设计的智力拼图玩具的一部分，现在明明遇到了两个问题，请你帮助解决：

问题1：∠D＝32°，∠ACD＝60°，为保证AB∥DE，则∠A等于多少度？

问题2：∠G，∠GFH，∠H之间有什么样的关系时，GP∥HQ?

Answer 1

【答案】28°，∠G＋∠GFH＋∠H＝360°

【解析】试题分析：（1）过C作CM∥AB，根据平行线的性质可得∠A=∠1=28°，再计算∠2=∠D=32°可得答案；

（2）当∠G+∠GFH+∠H=360°时，GP∥HQ；过F作FN∥GP，然后证明∠2+∠H=180°进而可得FN∥HQ，从而可证出GP∥HQ．

试题解析：（1）过点C作CM∥AB.

因为CM∥AB，所以∠ACM＝∠A.

因为AB∥DE，

所以CM∥DE.所以∠DCM＝∠D.

又因为∠ACD＝60°，

所以∠ACM＋∠DCM＝60°.

所以∠ACM＝60°－∠DCM＝60°－∠D＝60°－32°＝28°.

所以∠A＝28°时，AB∥DE.

（2）过点F作FN∥GP.

因为FN∥GP，

所以∠G＋∠GFN＝180°.

因为GP∥HQ，

所以FN∥HQ.所以∠H＋∠NFH＝180°.

所以∠G＋∠GFH＋∠H＝∠G＋∠GFN＋∠H＋∠NFH＝180°＋180°＝360°.

所以∠G＋∠GFH＋∠H＝360°时，GP∥HQ.

点睛: 此题主要考查了平行线的判定和性质，关键是掌握两直线平行，内错角相等，同旁内角互补．