Question

【题目】如图，△ABC中，∠ACB=90°，∠A=30°，AB=16．点P是斜边AB上一点．过点P作PQ⊥AB，垂足为P，交边AC（或边CB）于点Q，设AP=x，△APQ的面积为y，则y与x之间的函数图象大致为（ ）

A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：当点Q在AC上时，

∵∠A=30°，AP=x，

∴PQ=xtan30°= ，

∴y= ×AP×PQ= ×x× = x2；

当点Q在BC上时，如下图所示：

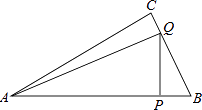
∵AP=x，AB=16，∠A=30°，

∴BP=16﹣x，∠B=60°，

∴PQ=BPtan60°= （16﹣x）．

∴ = = ．

∴该函数图象前半部分是抛物线开口向上，后半部分也为抛物线开口向下．

故答案为：B．

当点Q在AC上时AP=x，利用解直角三角形得出PQ的长度，利用三角形的面积公式得出Y与X的函数关系式；当点Q在BC上时，AP=x，AB=16，∠A=30°，BP=16﹣x，∠B=60°，PQ=BPtan60°，利用三角形的面积公式 S△APQ = AP PQ得出函数解析式，根据抛物线的开口方向从而得出结论。