题目内容
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上运动,点
上运动,点![]() 是坐标平面内的任意一点.若以
是坐标平面内的任意一点.若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是边长为5的菱形时,则点
为顶点的四边形是边长为5的菱形时,则点![]() 的坐标为__________.
的坐标为__________.

【答案】![]() 或
或![]() 或
或![]()
【解析】
因为点![]() 是坐标平面内的任意一点.若以
是坐标平面内的任意一点.若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是边长为5的菱形时,始终有△ODP是腰长为5的等腰三角形,而△ODP是腰长为5的等腰三角形有三种情况,要分类讨论求解即可.
为顶点的四边形是边长为5的菱形时,始终有△ODP是腰长为5的等腰三角形,而△ODP是腰长为5的等腰三角形有三种情况,要分类讨论求解即可.
解:由题意,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是边长为5的菱形时,始终有△ODP是腰长为5的等腰三角形,而当△ODP是腰长为5的等腰三角形时,有三种情况:
为顶点的四边形是边长为5的菱形时,始终有△ODP是腰长为5的等腰三角形,而当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如答图①所示,PD=OD=5,点P在点D的左侧.

过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE=![]() ,
,
∴OE=OD-DE=5-3=2,
∴此时点P坐标为(2,4);
(2)如答图②所示,OP=OD=5.
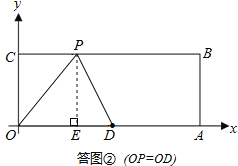
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得:OE=![]() ,
,
∴此时点P坐标为(3,4);
(3)如答图③所示,PD=OD=5,点P在点D的右侧.
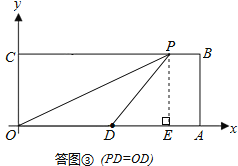
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE=![]()
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4).
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4);
故答案为:(2,4)或(3,4)或(8,4);

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





