题目内容
 如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为( )
如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为( )分析:根据平行四边形的对边相等、三角形的中位线定理“三角形的中位线等于第三边的一半”求解.
解答: 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴AB=CD;
又∵E、F分别是AD、BD的中点,
∴EF是△DAB的中位线,
∴EF=
AB,
∴EF=
CD=3,
∴CD=6;
故选B.
 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,∴AB=CD;
又∵E、F分别是AD、BD的中点,
∴EF是△DAB的中位线,
∴EF=
| 1 |
| 2 |
∴EF=
| 1 |
| 2 |
∴CD=6;
故选B.
点评:本题考查了平行四边形的性质、三角形中位线定理的综合运用.中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=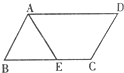 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.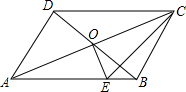 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是