题目内容
(2012•长春一模)感知:如图①,在菱形ABCD中,AB=BD,点E、F分别在边AB、AD上.若AE=DF,易知△ADE≌△DBF.
探究:如图②,在菱形ABCD中,AB=BD,点E、F分别在BA、AD的延长线上.若AE=DF,△ADE与△DBF是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展:如图③,在?ABCD中,AD=BD,点O是AD边的垂直平分线与BD的交点,点E、F分别在OA、AD的延长线上.若AE=DF,∠ADB=50°,∠AFB=32°,求∠ADE的度数.

探究:如图②,在菱形ABCD中,AB=BD,点E、F分别在BA、AD的延长线上.若AE=DF,△ADE与△DBF是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展:如图③,在?ABCD中,AD=BD,点O是AD边的垂直平分线与BD的交点,点E、F分别在OA、AD的延长线上.若AE=DF,∠ADB=50°,∠AFB=32°,求∠ADE的度数.

分析:探究:△ADE和△DBF全等,利用菱形的性质首先证明三角形ABD为等边三角形,再利用全等三角形的判定方法即可证明△ADE≌△DBF;
拓展:因为点O在AD的垂直平分线上,所以OA=OD,再通过证明△ADE≌△DBF,利用全等三角形的性质即可求出∠ADE的度数.
拓展:因为点O在AD的垂直平分线上,所以OA=OD,再通过证明△ADE≌△DBF,利用全等三角形的性质即可求出∠ADE的度数.
解答:解:
探究:△ADE和△DBF全等.
∵四边形ABCD是菱形,
∴AB=AD.
∵AB=BD,
∴AB=AD=BD.
∴△ABD为等边三角形.
∴∠DAB=∠ADB=60°.
∴∠EAD=∠FDB=120°.
∵AE=DF,
∴△ADE≌△DBF;
拓展:
∵点O在AD的垂直平分线上,
∴OA=OD.
∴∠DAO=∠ADB=50°.
∴∠EAD=∠FDB.
∵AE=DF,AD=DB,
∴△ADE≌△DBF.
∴∠DEA=∠AFB=32°.
∴∠EDA=18°.
探究:△ADE和△DBF全等.
∵四边形ABCD是菱形,
∴AB=AD.
∵AB=BD,
∴AB=AD=BD.
∴△ABD为等边三角形.
∴∠DAB=∠ADB=60°.
∴∠EAD=∠FDB=120°.
∵AE=DF,
∴△ADE≌△DBF;
拓展:
∵点O在AD的垂直平分线上,
∴OA=OD.
∴∠DAO=∠ADB=50°.
∴∠EAD=∠FDB.
∵AE=DF,AD=DB,
∴△ADE≌△DBF.
∴∠DEA=∠AFB=32°.
∴∠EDA=18°.
点评:本题考查了菱形的性质、等边三角形的判定和性质以及全等三角形的判定和性质,题目综合性很强,但难度不大.

练习册系列答案
相关题目
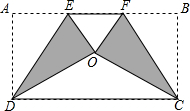 (2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则
(2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则 (2012•长春一模)如图,抛物线y=ax2-x-
(2012•长春一模)如图,抛物线y=ax2-x- -B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)
-B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)