Question

（2011•犍为县模拟）甲题：已知关于x的一元二次方程x²=2（1-m）x-m²的两实数根为x₁，x₂．
（1）求m的取值范围；
（2）设y=x₁+x₂，当y取得最小值时，求相应m的值，并求出最小值．
乙题：如图，在?ABCD中，BE⊥AD于点E，BF⊥CD于点F，AC与BE、BF分别交于点G，H．
（1）求证：△BAE∽△BCF．
（2）若BG=BH，求证：四边形ABCD是菱形．

Answer 1

分析：甲题：（1）若一元二次方程有两不等根，则根的判别式△=b²-4ac≥0，建立关于m的不等式，可求出m的取值范围；
（2）根据根与系数的关系可得出x₁+x₂的表达式，进而可得出y、m的函数关系式，根据函数的性质及（1）题得出的自变量的取值范围，即可求出y的最小值及对应的m值；
乙题：（1）先利用已知里的两个垂直，可证一对角相等，都等于90°，再利用平行四边形的性质，对角相等，那么可证△BAE∽△BCF；
（2）由BG=BH，可得∠3=∠4，那么∠AGE=∠CHF，利用等量减等量差相等，可证∠DAC=∠DCA，等角对等边，那么AD=DC，那么?是菱形．

解答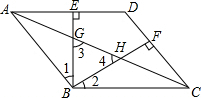：甲题．
解：（1）将原方程整理为 x²+2（m-1）x+m²=0．
∵原方程有两个实数根，
∴△=[2（m-1）]²-4m²=-8m+4≥0，得 m≤

1

2

．…（5分）
（2）∵x₁，x₂为x²+2（m-1）x+m²=0的两根，
∴y=x₁+x₂=-2m+2，且m≤

1

2

．
因而y随m的增大而减小，故当m=

1

2

时，取得极小值1．…（10分）

乙题．
证明（1）∵BE⊥AD，BF⊥CD
∴∠BEA=∠BFC=90°
又∵ABCD是平行四边形，
∴∠BAE=∠BCF
∴△BAE∽△BCF …（5分）
（2）∵△BAE∽△BCF∴∠1=∠2…（6分）
又∵BG=BH
∴∠3=∠4
∴∠BGA=∠BHC …（7分）
∴△BGA≌△BHC（ASA）  …（8分）
∴AB=BC
∴四边形ABCD为菱形 …（10分）

点评：甲题考查的知识点是根的判别式、根与系数的关系与一次函数的结合题．牢记一次函数的性质是解答（2）题的关键；
乙题考查的知识点是相似三角形的判定与性质、平行四边形的性质及菱形的判定，关键利用了平行四边形的性质、相似三角形的判定和性质、全等三角形的判定和性质、菱形的判定等知识．