题目内容
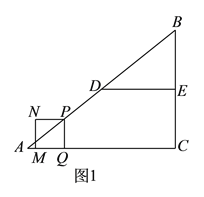
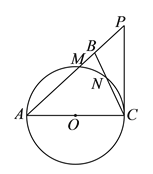
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的⊙
为直径的⊙![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
(![]() )求证:直线
)求证:直线![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )若
)若![]() ,
,![]() ,求点
,求点![]() 到
到![]() 的距离.
的距离.
(![]() )在第(
)在第(![]() )的条件下,求
)的条件下,求![]() 的周长.
的周长.
【答案】(1)证明见解析;(2)点![]() 到
到![]() 的距离为
的距离为![]() ;(3)
;(3)![]() 的周长为
的周长为![]() .
.
【解析】试题分析:(1)根据∠ABC=∠ACB且∠CAB=2∠BCP,在△ABC中∠ABC+∠BAC+∠BCA=180°,得到2∠BCP+2∠BCA=180°,从而得到∠BCP+∠BCA=90°,证得直线CP是 O的切线.(2)作BD⊥AC于点D,得到BD∥PC,从而利用sin∠BCP=sin∠DBC=![]() ,求得DC=2,再根据勾股定理求得点B到AC的距离为4.(3)先求出AC的长度,然后利用BD∥PC的比例线段关系求得CP的长度,再由勾股定理求出AP的长度,从而求得△ACP的周长.
,求得DC=2,再根据勾股定理求得点B到AC的距离为4.(3)先求出AC的长度,然后利用BD∥PC的比例线段关系求得CP的长度,再由勾股定理求出AP的长度,从而求得△ACP的周长.
试题解析:(![]() )∵
)∵![]() 且
且![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵点![]() 在直径上,
在直径上,
∴直线![]() 是
是![]() 的切线.
的切线.
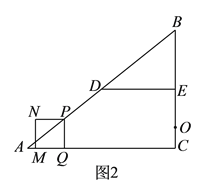
(![]() )如图,作
)如图,作![]() 于
于![]() ,
,
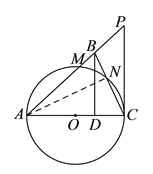
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴由勾股定理得![]() ,
,
∴点![]() 到
到![]() 的距离为
的距离为![]() .
.
(![]() )连接
)连接![]() ,∵
,∵![]() 为直径,
为直径,
∴![]() ,
,
∴![]() 中,
中,
![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]()
在![]() 中,
中,![]() ,
,
![]() ,
,
∴![]() 的周长为
的周长为![]() .
.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目