题目内容
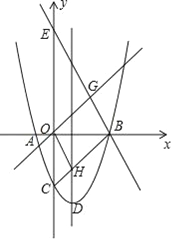
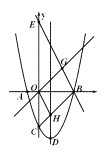
【题目】如图,抛物线y=x2﹣(m+2)x+3(m﹣1)与x轴的两个交点为A、B,与y轴交于点C,点D为抛物线的顶点,直线y=﹣2x+m+6经过点B,交y轴于点E(0,6).
(1)求直线和抛物线的解析式;
(2)如果抛物线的对称轴与线段BC交于点H,且直线y=x与直线y=﹣2x+m+6交于点G,求证:四边形OHBG是平行四边形;
(3)在抛物线上是否存在点P,使△APB的面积等于平行四边形OHBG的面积,若存在,直接写出P点的坐标,若不存在请说明理由.
【答案】(1)y=x2-2x-3;(2)证明见解析(3)存在满足条件的点p,点p的坐标是(0,-3)或(2,-3)或(1+![]() ,3)
,3)
【解析】试题分析:(1)根据待定系数法,可求得答案;
(2)根据直线的一次项的系数相等,可得平行线,根据平行四边形的定义可得结果;
(3)根据面积相等,可得关于x的方程,根据解方程,可得点的坐标.
试题解析:(1)将点E(0,6)代入直线y=-2x+m+6得
M+6=6,则m=0,∴直线的解析式为y=-2x+6,
抛物线的解析式为y=x2-2x-3;
(2)∵y=x2-2x-3=(x+1)(x-3)=(x-1)2-4
∴B(3,0),C(0,-3),D(1,-4),对称轴为x=1
设直线BC的解析式为y=kx-3
则3k-3=0,即k=1,∴直线BC的解析式为y=x-3
则BC∥OG,点H的坐标为(1,-2)
设直线OH的解析式为y=ax,则a=-2,∴直线OH的解析式为y=-2x,
∴OH∥BG,∴四边形OHBG是平行四边形;
(3)存在满足条件的点p,点p的坐标是(0,-3)或(2,-3)或(1+![]() ,3)
,3)
∵OB=3,△OBH的OB边上的高为2,
∴平行四边形的面积=2x![]() x3x2=6
x3x2=6
设点P的坐标为(x,x2-2x-3)
∵AB=4,∴![]() ×4|x2-2x-3|=6,解得x=1±
×4|x2-2x-3|=6,解得x=1±![]() 或x=0或x=2
或x=0或x=2
∴P的坐标为(0,-3)或(2,-3)或(1-![]() ,3)或(1+
,3)或(1+![]() ,3)
,3)

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案