题目内容
【题目】如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=![]() ﹣1,则∠ACD= °.
﹣1,则∠ACD= °.
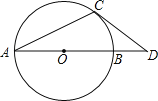
【答案】112.5.
【解析】
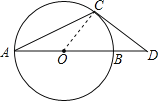
试题分析:如图,连结OC.根据切线的性质得到OC⊥DC,根据线段的和得到OD=![]() ,根据勾股定理得到CD=1,根据等腰直角三角形的性质得到∠DOC=45°,根据等腰三角形的性质和三角形外角的性质得到∠OCA=
,根据勾股定理得到CD=1,根据等腰直角三角形的性质得到∠DOC=45°,根据等腰三角形的性质和三角形外角的性质得到∠OCA=![]() ∠DOC=22.5°,再根据角的和得到∠ACD的度数.
∠DOC=22.5°,再根据角的和得到∠ACD的度数.
解:如图,连结OC.
∵DC是⊙O的切线,
∴OC⊥DC,
∵BD=![]() ﹣1,OA=OB=OC=1,
﹣1,OA=OB=OC=1,
∴OD=![]() ,
,
∴CD=![]() =
=![]() =1,
=1,
∴OC=CD,
∴∠DOC=45°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=![]() ∠DOC=22.5°,
∠DOC=22.5°,
∴∠ACD=∠OCA+∠OCD=22.5°+90°=112.5°.
故答案为:112.5.

练习册系列答案
相关题目