题目内容
【题目】如图，观察二次函数y=ax2+bx+c的图象，下列结论：
①a+b+c＞0，②2a+b＞0，③b2﹣4ac＞0，④ac＞0．
其中正确的是（ ）
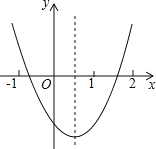
A．①② B．①④ C．②③ D．③④
【答案】C
【解析】
试题分析：令x=1代入可判断①；由对称轴x=﹣
的范围可判断②；由图象与x轴有两个交点可判断③；由开口方向及与x轴的交点可分别得出a、c的符号，可判断④．
解：由图象可知当x=1时，y＜0，
∴a+b+c＜0，
故①不正确；
由图象可知0＜﹣＜1，
∴＞﹣1，
又∵开口向上，
∴a＞0，
∴b＞﹣2a，
∴2a+b＞0，
故②正确；
由图象可知二次函数与x轴有两个交点，
∴方程ax2+bx+c=0有两个不相等的实数根，
∴△＞0，即b2﹣4ac＞0，
故③正确；
由图象可知抛物线开口向上，与y轴的交点在x轴的下方，
∴a＞0，c＜0，
∴ac＜0，
故④不正确；
综上可知正确的为②③，
故选C．
练习册系列答案
相关题目
