题目内容
【题目】操作:将一把三角尺放在如图①的正方形![]() 中,使它的直角顶点
中,使它的直角顶点![]() 在对角线
在对角线![]() 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点![]() ,另一边与射线
,另一边与射线![]() 相交于点
相交于点![]() ,探究:
,探究:
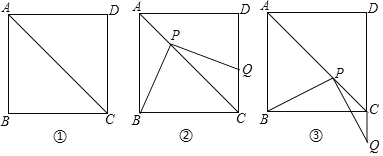
(1)如图②,当点![]() 在
在![]() 上时,求证:
上时,求证:![]() .
.
(2)如图③,当点![]() 在
在![]() 延长线上时,①中的结论还成立吗?简要说明理由.
延长线上时,①中的结论还成立吗?简要说明理由.
【答案】(1)证明见解析;(2)成立,理由见解析.
【解析】
(1)过点P作MN//BC,可以证明△PMQ≌△BNP,从而得出BP=QP;
(2)过点![]() 作
作![]() 于
于![]() ,
,![]() 交
交![]() 于点
于点![]() ,可以证明△PMQ≌△BNP,从而得出BP=QP;
,可以证明△PMQ≌△BNP,从而得出BP=QP;
(1)证明:过点![]() 作
作![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,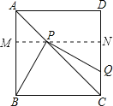
则四边形AMND和四边形BCNM都是矩形,△AMP和△CNP都是等腰直角三角形.
∴NP=NC=MB
∵∠BPQ=90°
∴∠QPN+∠BPM=90°,而∠BPM+∠PBM=90° ,
∴∠QPN=∠PBM,又∠QNP=∠PMB=90°,
在△QNP和△BMP中,
∠QNP=∠PMB,MB=NP,∠QPN=∠PBM
∴△QNP≌△PMB(ASA),
∴PQ=BP.
(2)成立.
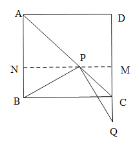
过点![]() 作
作![]() 于
于![]() ,
,![]() 交
交![]() 于点
于点![]()
在正方形![]() 中
中![]() ,
,![]()
∴![]()
∴![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,![]()
∴![]() ,
,
在![]() 和
和![]() 中,
中,
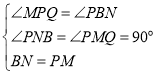 ,
,
∴![]() ,
,
∴![]() ;
;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目