题目内容
【题目】如图,ABCD中,AB=2cm,AC=5cm,SABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,同时,点F从D点出发,以同样的速度在CD延长线上向左运动,运动时间为t秒.
(1)在运动过程中,四边形AECF的形状是____;
(2)t=____时,四边形AECF是矩形;
(3)求当t等于多少时,四边形AECF是菱形.

【答案】(1)四边形AECF是平行四边形;理由见解析;(2)t=1;(3)t=![]()
【解析】
(1)由平行四边形的性质得出AB=CD=2cm,AB∥CD,由已知条件得出CF=AE,即可得出四边形AECF是平行四边形;
(2)若四边形AECF是矩形,则∠AFC=90°,得出AF⊥CD,由平行四边形的面积得出AF=4cm,在Rt△ACF中,由勾股定理得出方程,解方程即可;
(3)当AE=CE时,四边形AECF是菱形.过C作CG⊥BE于G,则CG=4cm,由勾股定理求出AG,得出GE,由勾股定理得出方程,解方程即可.
解:(1)四边形AECF是平行四边形;理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD=2cm,AB∥CD,
∴CF∥AE,
∵DF=BE,
∴CF=AE,
∴四边形AECF是平行四边形;
故答案为:平行四边形;
(2)t=1时,四边形AECF是矩形;理由如下:
若四边形AECF是矩形,
∴∠AFC=90°,
∴AF⊥CD,
∵SABCD=CDAF=8cm2,
∴AF=4cm,
在Rt△ACF中,AF2+CF2=AC2,
即42+(t+2)2=52,
解得:t=1,或t=-5(舍去),
∴t=1;故答案为:1;
(3)依题意得:AE平行且等于CF,
∴四边形AECF是平行四边形,
故AE=CE时,四边形AECF是菱形.
又∵BE=tcm,
∴AE=CE=t+2(cm),
过C作CG⊥BE于G,如图所示:
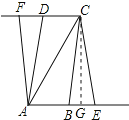
则CG=4cm
AG=![]() =3(cm),
=3(cm),
∴GE=t+2-3=t-1(cm),
在△CGE中,由勾股定理得:CG2+GE2=CE2=AE2,
即42+(t-1)2=(t+2)2,
解得:t=![]() ,
,
即t=![]() s时,四边形AECF是菱形.
s时,四边形AECF是菱形.