题目内容
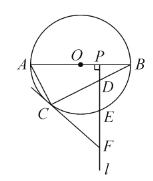
【题目】如图,![]() 是☉
是☉![]() 的直径,
的直径,![]() 为☉
为☉![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,则
,则![]() _________.
_________.
【答案】(1)详见解析;(2)①以![]() 为顶点的四边形是菱形;②9
为顶点的四边形是菱形;②9
【解析】
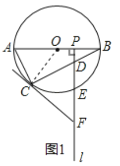
(1)连接OC,根据切线的性质得出OC⊥CF以及∠OBC=∠OCB得∠FCD=∠FDC,可证得结论;
(2)①如图2,连接OC,OE,BE,CE,可证△BOE,△OCE均为等边三角形,可得OB=BE=CE=OC,可得结论;
②设AC=3k,BC=4k(k>0),由勾股定理可求k=6,可得AC=18,BC=24,由面积法可求PE,由勾股定理可求OP的长.
(1)证明:如图1,连接![]() ,则
,则![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() .
.
(2)解:如图2,连接![]() 与
与![]() 交于点
交于点![]() .
.
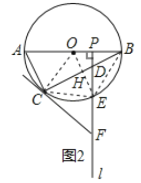
①以![]() 为顶点的四边形是菱形.理由如下:
为顶点的四边形是菱形.理由如下:
![]() 是直径,
是直径,
![]() .
.
![]() ,
,
![]() .
.
![]() 是
是![]() 的中点,
的中点,
![]() .
.
又![]() ,
,
![]() 均为等边三角形,
均为等边三角形,
![]() ,
,
![]() 四边形
四边形![]() 是菱形.
是菱形.
②![]()
![]() 设
设![]() ,则
,则![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() ,即
,即![]() ,
,
解得![]() ,
,
![]() .
.
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() .
.
故答案为:9.

练习册系列答案
相关题目