题目内容
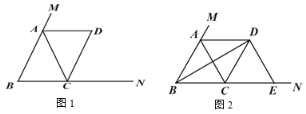
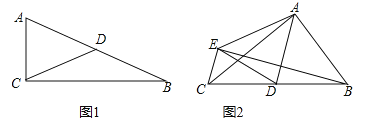
【题目】阅读理解:我们学习过直角三角形斜边上的中线等于斜边的一半,即:如图1,在![]() 中,
中,![]() ,若点
,若点![]() 是斜边
是斜边![]() 的中点,则
的中点,则![]()
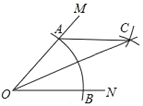
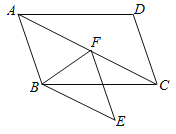
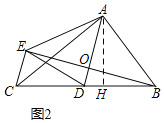
灵活应用:如图2,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() 连接
连接![]() .
.
(1)线段![]() 的长是 ;
的长是 ;
(2)判断![]() 的形状并说明理由;
的形状并说明理由;
(3)线段![]() 的长是 .
的长是 .
【答案】(1)![]() ;(2)△BCE是直角三角形,理由见解析;(3)
;(2)△BCE是直角三角形,理由见解析;(3)![]()
【解析】
(1)依据勾股定理进行计算即可得到BC的长,再根据直角三角形斜边上中线的性质即可得到结论;
(2)依据CD=DE=DB,可得∠DEC=∠DCE,∠DEB=∠DBE,再根据三角形内角和定理,即可得出∠DEB+∠DEC=90°,进而得到△BCE是直角三角形;
(3)利用![]() BCAH=
BCAH=![]() ABAC,可得AH=
ABAC,可得AH=![]() ,依据AD垂直平分线段BE,可得
,依据AD垂直平分线段BE,可得![]() ADBO=
ADBO=![]() BDAH,即可得出OB=
BDAH,即可得出OB=![]() ,BE=2OB=
,BE=2OB=![]() ,最后在Rt△BCE中,运用勾股定理可得EC=
,最后在Rt△BCE中,运用勾股定理可得EC=![]() .
.
解:(1)在Rt△ABC中,∠BAC=90°,AB=3,AC=4,
由勾股定理得,BC=![]() ,
,
∵点D是BC的中点,BCRt△ABC的斜边,
∴AD=![]() BC=
BC=![]() ;
;
(2)△BCE为直角三角形.理由:
∵D是BC的中点
∴CD=BD
∵将△ABD沿AD翻折得到△AED,
∴DE=DB,
∴CD=DE=DB,
∴∠DEC=∠DCE,∠DEB=∠DBE,
∵∠DEC+∠DCE+∠DEB+∠DBE=180°,
∴∠DEB+∠DEC=90°,
∴∠BEC=90°,
∴△BCE是直角三角形;
(3)如图,连接BE交AD于O,作AH⊥BC于H.
由题可得AD=DC=DB=![]() ,
,
∵![]() BCAH=
BCAH=![]() ABAC,
ABAC,
∴AH=![]() ,
,
∵AE=AB,DE=DB,
∴点A在BE的垂直平分线上,点D在BE的垂直平分线上,
∴AD垂直平分线段BE,
∵![]() ADBO=
ADBO=![]() BDAH,
BDAH,
∴OB=![]() ,
,
∴BE=2OB=![]() ,
,
在Rt△BCE中,EC=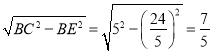 .
.

 口算题天天练系列答案
口算题天天练系列答案【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是x与y的几组对应值.
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
|
| m | ... |
求m的值;
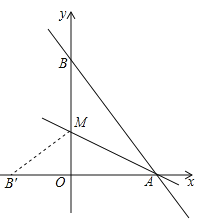
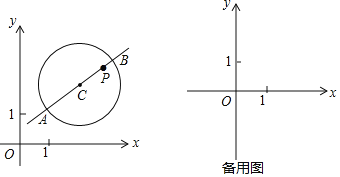
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,![]() ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).