题目内容
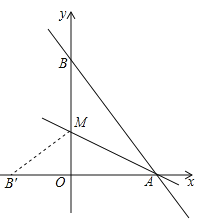
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() 是
是![]() 上的一点,若将
上的一点,若将![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 轴上的点
轴上的点![]() 处,则点
处,则点![]() 的坐标为______.
的坐标为______.
【答案】(0,3)
【解析】
由解析式令x=0,![]() =8,即B(0,8),令y=0时,x=6,即A(6,0),再根据勾股定理即可得出AB的长,由折叠的性质,可求得AB′与OB′的长,BM=B′M,然后设MO=x,由在Rt△OMB′中,OM2+OB′2=B′M2,求出M的坐标.
=8,即B(0,8),令y=0时,x=6,即A(6,0),再根据勾股定理即可得出AB的长,由折叠的性质,可求得AB′与OB′的长,BM=B′M,然后设MO=x,由在Rt△OMB′中,OM2+OB′2=B′M2,求出M的坐标.
解:当x=0时,![]() =8,即B(0,8),
=8,即B(0,8),
当y=0时,x=6,即A(6,0),
∴AB=![]() ,
,
由折叠的性质,得:AB=AB′=10,
∴OB′=AB′-OA=10-6=4,
设MO=x,则MB=MB′=8-x,
在Rt△OMB′中,OM2+OB′2=B′M2,
即x2+42=(8-x)2,
解得:x=3,
∴M(0,3).
故答案为:(0,3).

练习册系列答案
相关题目