题目内容
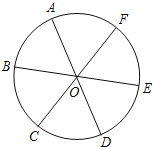
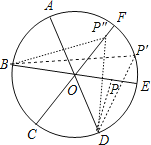
【题目】如图，点A、B、C、D、E、F为⊙O的六等分点，动点P从圆心O出发，沿OE弧EFFO的路线做匀速运动，设运动的时间为t，∠BPD的度数为y，则下列图象中表示y与t之间函数关系最恰当的是（ ）
A．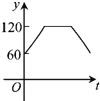
B．
C．
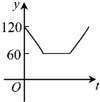D．
【答案】C
【解析】
试题分析：利用点A、B、C、D、E、F为⊙O的六等分点可得到∠BOC=∠COD=60°，所以P在O点时，∠BPD=120°，P在弧EF上时，∠BPD=
∠BOD=60°，然后分类讨论：当点P从O点运动到E点时，易得y由120°逐渐减小到60°；当点P在弧EF上运动时，y=60°；当点P从F点运动到O点时，易得y由60°逐渐增大到120°，根据此特征可对四个选项进行判断．
解：因为点A、B、C、D、E、F为⊙O的六等分点，
所以∠BOC=∠COD=60°，
当P在O点时，∠BPD=120°，当P在弧EF上时，∠BPD=∠BOD=60°，
当点P从O点运动到E点时，y由120°逐渐减小到60°；当点P在弧EF上运动时，y的值不变，为60°；当点P从F点运动到O点时，y由60°逐渐增大到120°．
故选C．
练习册系列答案
同步练习强化拓展系列答案
相关题目
【题目】小明同学在用描点法画二次函数y=ax2+bx+c图象时，由于粗心，他算错了一个y值，列出了下面表格：
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | 5 | 3 | 2 | 3 | 6 | … |
（1）请指出这个错误的y值，并说明理由；
（2）若点M（a，y1），N（a+4，y2）在二次函数y=ax2+bx+c图象上，且a＞﹣1，试比较y1与y2的大小．
