题目内容
【题目】小明同学在用描点法画二次函数y=ax2+bx+c图象时，由于粗心，他算错了一个y值，列出了下面表格：
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | 5 | 3 | 2 | 3 | 6 | … |
（1）请指出这个错误的y值，并说明理由；
（2）若点M（a，y1），N（a+4，y2）在二次函数y=ax2+bx+c图象上，且a＞﹣1，试比较y1与y2的大小．
【答案】（1）5；（2）y1＞y2
【解析】
试题分析：（1）根据关于对称轴对称的自变量对应的函数值相等，可得答案．
（2）分三种情况讨论：①﹣1＜a＜1；②a=1；③a＞1；分别比较y1与y2大小．
解：（1）由函数图象关于对称轴对称，得
（0，3），（1，2），（2，3）在函数图象上，
把（0，3），（1，2），（2，3）代入函数解析式，得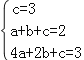
，
解得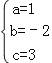
，
函数解析式为y=x2﹣2x+3，
x=﹣1时y=6，
故y错误的数值为5．
（2）分三种情况讨论：
①﹣1＜a＜1时，M（a，y1）离对称轴的距离小于N（a+4，y2）离对称轴的距离，
所以y1＜y2；
②a=1时，M（a，y1）离对称轴的距离等于N（a+4，y2）离对称轴的距离，
所以y1=y2；
③a＞1时，M（a，y1）离对称轴的距离小于N（a+4，y2）离对称轴的距离，
所以y1＞y2．
练习册系列答案
相关题目
