题目内容
【题目】在△ABC中，∠B=25°，AD是BC边上的高，并且AD2=BDCD，则∠BCA的度数为多少？
【答案】65°或115°．
【解析】
试题分析：解答此题的关键的是利用AD2=BD×CD，推出△ABD∽△ADC，然后利用对应角相等即可知∠BCA的度数．注意分为高在三角形内与高在三角形外两种．
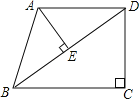
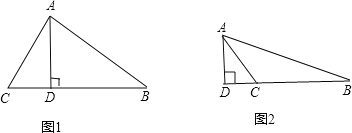
解：如图1：∵∠B=25°，AD是BC边上的高，
∴∠BAD=65°，
∵AD2=BD．CD，
∴
，AD⊥BC，
∴△ABD∽△CDA，
∴∠BCA=∠BAD=65°．
如图2：∵∠B=25°，AD是BC边上的高，
∴∠BAD=65°，
∵AD2=BD．CD，
∴，AD⊥BC，
∴△ABD∽△CDA，
∴∠ACD=∠BAD=65°，
∴∠ACB=180°﹣∠ACD=115°．
∴∠BCA的度数为65°或115°．
练习册系列答案
同步奥数系列答案
相关题目
