题目内容
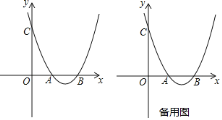
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知二次函数的图象经过点
,已知二次函数的图象经过点![]() 、
、![]() 和点
和点![]() .
.

![]() 求
求![]() 、
、![]() 两点坐标;
两点坐标;
![]() 求该二次函数的关系式
求该二次函数的关系式
![]() 若抛物线的对称轴与
若抛物线的对称轴与![]() 轴的交点为点
轴的交点为点![]() ,则在抛物线的对称轴上是否存在点
,则在抛物线的对称轴上是否存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形?如果存在,直接写出
为腰的等腰三角形?如果存在,直接写出![]() 点的坐标;如果不存在,请说明理由;
点的坐标;如果不存在,请说明理由;
![]() 点
点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线与抛物线相交于点
轴的垂线与抛物线相交于点![]() ,当点
,当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出四边形
的面积最大?求出四边形![]() 的最大面积及此时
的最大面积及此时![]() 点的坐标.
点的坐标.
【答案】![]() 点
点![]() ,
,![]() ;
;![]()
![]() ;
;![]()
![]() ,
,![]() ,
,![]() ;
;![]()
![]()
【解析】
(1)分别令解析式![]() 中x=0和y=0,求出点B、点C的坐标;
中x=0和y=0,求出点B、点C的坐标;
(2)设二次函数的解析式为![]() ,将点A、B、C的坐标代入解析式,求出a、b、c的值,进而求得解析式;
,将点A、B、C的坐标代入解析式,求出a、b、c的值,进而求得解析式;
(3)由(2)的解析式求出顶点坐标,再由勾股定理求出CD的值,再以点C为圆心,CD为半径作弧交对称轴于P1,以点D为圆心CD为半径作圆交对称轴于点P2,P3,作CE垂直于对称轴与点E,由等腰三角形的性质及勾股定理就可以求出结论;
(4)设出E点的坐标为(a![]() ),就可以表示出F的坐标,由四边形CDBF的面积=S△BCD+S△CEF+S△BEF求出S与a的关系式,由二次函数的性质就可以求出结论.
),就可以表示出F的坐标,由四边形CDBF的面积=S△BCD+S△CEF+S△BEF求出S与a的关系式,由二次函数的性质就可以求出结论.
![]() 令
令![]() ,可得
,可得![]() ,
,
令![]() ,可得
,可得![]() ,
,
即点![]() ,
,![]() ;
;![]() 设二次函数的解析式为
设二次函数的解析式为![]() ,
,
将点![]() 、
、![]() 、
、![]() 的坐标代入解析式得,
的坐标代入解析式得,
 ,
,
解得: ,
,

即该二次函数的关系式为![]() ;
;![]() ∵
∵![]() ,
,
∴![]() ,
,
∴抛物线的对称轴是![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得
![]() .
.
∵![]() 是以
是以![]() 为腰的等腰三角形,
为腰的等腰三角形,
∴![]() .
.
如图![]() 所示,作
所示,作![]() 对称轴于
对称轴于![]() ,
,
∴![]() ,
,
∴![]() .
.

∴![]() ,
,![]() ,
,![]() ;
;![]() 当
当![]() 时,
时,![]()
∴![]() ,
,![]() ,
,
∴![]() .
.
∵直线![]() 的解析式为:
的解析式为:![]() .
.
如图![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,设
,设![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
![]() ,
,
![]() .
.
![]()
∴![]() 时,
时,![]() ,
,
∴![]() .
.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目