题目内容
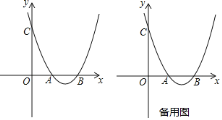
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
![]() 填空:
填空:![]() ________;
________;
![]() 点
点![]() 在抛物线上,且
在抛物线上,且![]() ,求
,求![]() 面积的最大值;
面积的最大值;
![]() 设
设![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ,一动点
,一动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒一个单位速度运动到
以每秒一个单位速度运动到![]() 点,再沿线段
点,再沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止,当点
后停止,当点![]() 的坐标是多少时,点
的坐标是多少时,点![]() 在整个运动中用时最少?
在整个运动中用时最少?
【答案】(1)-3(2)当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() (3)
(3)![]()
【解析】
(1)将点A的坐标代入得2+2m+4=0,然后,再求得m的值即可;
(2)先求得点B和点C的坐标,当0<a<4时,过点P作x轴的垂线交BC于D.设直线BC的解析式为y=kx+4,将点B的坐标代入可求得BC的解析式,设点P的坐标为(a,![]() ,则点D的坐标为(a,-a+4).然后由S△PBC=S△PCD+S△PBD可得到△PBC的面积与a的函数关系式,从而可得到△PBC的面积的最大值,当4≤a≤6时,过点P作y轴的垂线交BC于E.则E
,则点D的坐标为(a,-a+4).然后由S△PBC=S△PCD+S△PBD可得到△PBC的面积与a的函数关系式,从而可得到△PBC的面积的最大值,当4≤a≤6时,过点P作y轴的垂线交BC于E.则E![]() ,PE=
,PE=![]() ,然后依据S△PBC=S△PCE+S△PBE可得到△PBC的面积与a的函数关系式,从而可得到△PBC的面积的最大值;
,然后依据S△PBC=S△PCE+S△PBE可得到△PBC的面积与a的函数关系式,从而可得到△PBC的面积的最大值;
(3)作点A关于BC的对称点A′,过点A′作A′F⊥y轴,垂足为F,交BC与点H,依据轴对称的性质可得到A′(4,2)将y=2代入直线BC的解析式可得到点H的坐标.
(1)![]() ①当
①当![]() 时,过点
时,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于
于![]() .
.

令![]() 得:
得:![]() ,解得
,解得![]() 或
或![]() ,
,
∴![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,将点
,将点![]() 的坐标代入得:
的坐标代入得:![]() ,解得
,解得![]() ,
,
∴![]() 的解析式为
的解析式为![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .
.
∴![]() .
.
∴![]() .
.
当![]() 时
时![]() 最大值为
最大值为![]() .
.
②当![]() 时,过点
时,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于
于![]() .
.

∴![]() ,
,![]() .
.
∴![]() .
.
当![]() 时
时![]() 最大值为
最大值为![]() .
.
综上可知,当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() .
.![]() 作点
作点![]() 关于
关于![]() 的对称点
的对称点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交
,交![]() 与点
与点![]() .
.

∵![]() 的解析式为
的解析式为![]() .
.
∴![]() .
.
∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,即
,即![]() ,
,
∴点![]() 在整个运动中所用的时间为
在整个运动中所用的时间为![]() .
.
∴当点![]() 、
、![]() 、
、![]() 在一条直线上时,所用时间最短.
在一条直线上时,所用时间最短.
将![]() 代入
代入![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.