题目内容
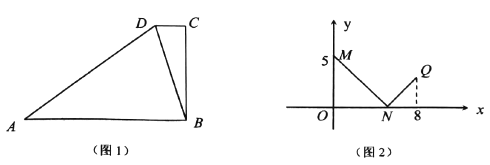
【题目】如图(如图1所示)在△ABC中,∠ACB=90°,∠A=30°,BC=4,沿斜边AB的中线CD把这个三角形剪成△AC1D1和△BC2D2两个三角形(如图2所示).将△AC1D1沿直线D2B方向平移(点A,D1,D2,B始终在同一直线上),当点D1于点B重合时,平移停止.设平移距离D1D2为x,△AC1D1和△BC2D2的重叠部分面积为y,在y与x的函数图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
【答案】C
【解析】如图3,当0≤x≤4时,
∵D2D1=x
∴D1E=BD1=D2F=AD2=4﹣x,
∴C2F=C1E=x.
∵在△ABC中,∠ACB=90°,∠A=30°,BC=4,
∴∠B=60°,
过C作CH⊥AB于H,
∴CH=2![]() ,
,
∵在△ABC中,sin∠CDB=![]() ,
,
∴sin∠ED1B=![]() =
=![]() .
.
设△BED1的BD1边上的高为h,
∴h=![]() ,
,
∴S△BD1E=![]() ×BD1×h=
×BD1×h=![]() (4﹣x)2.
(4﹣x)2.
∵∠C1+∠C2=90°,
∴∠FPC2=90°.
∵∠C2=∠B,
∴sin∠B=![]() ,cos∠B=
,cos∠B=![]() ,
,
∴PC2=![]() x,PF=
x,PF=![]() x,
x,
∴S△FC2P=![]() PC2PF=
PC2PF=![]() x2
x2
∴y=S△D2C2B﹣S△BD1E﹣S△FC2P=![]() (4﹣x)﹣
(4﹣x)﹣![]() (4﹣x)2﹣
(4﹣x)2﹣![]() x2=﹣
x2=﹣![]() x2+
x2+![]() x
x
∴y=﹣![]() x2+
x2+![]() x.
x.
∴y与x的函数图象大致是C选项,
故选:C.


练习册系列答案
相关题目