题目内容
阅读并解答下列问题：我们熟悉两个乘法公式：①（
+b）2=2+2b+b2;②(-b)2=2-2b+b2.现将这两个公式变形，可得到一个新的公式③：b=(
)2-(
)2, 这个公式形似平方差公式，我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。
例如：因式分解：（b-1）2+(+b-2)( +b-2b)
解：原式=
+
-
=(b-1)2+(+b-b-1)2-(b-1)2=(-1)(b-1)2=（-1）2(b-1)2你能利用公式（或其他方法）解决下列问题吗？
已知各实数，b，c满足b=c2+9且=6-b，求证：="b"
+b）2=2+2b+b2;②(-b)2=2-2b+b2.现将这两个公式变形，可得到一个新的公式③：b=()2-()2, 这个公式形似平方差公式，我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。例如：因式分解：（
b-1）2+(+b-2)( +b-2b) 解：原式=
+-=(
b-1)2+(+b-b-1)2-(b-1)2=(-1)(b-1)2=（-1）2(b-1)2你能利用公式（或其他方法）解决下列问题吗？已知各实数
，b，c满足b=c2+9且=6-b，求证：="b" 通过化简分析进而求解
试题分析：已知a+b=6,(
)2-()2=c2+9,9-()2=c2+9,(
)2=c2=0,a-b=0,∴a=b.点评：解答本题的关键是熟练掌握任何非0数的0次幂为1；两个式子的积为0，则这两个式子至少有一个为0.,
练习册系列答案
相关题目
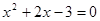，下列配方结果正确的是（ ）．
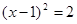
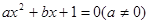有两个相等的实数根，求
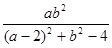的值.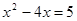
时，方程的两边同加上 ，使得方程左边配成一个完全平方式
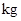，根据市场需要，今年该农场扩大了种植面积，并且全部种植了高产的新品种南瓜，已知南瓜种植面积的增长率是亩产量的增长率的2倍，今年南瓜的总产量为60 000kg，求南瓜亩产量的增长率．
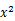-2x=0的解为 .