题目内容
若m为自然数,且4<m<40,且方程x2-2(2m-3)x+4m2-14m+8=0的两根均为整数,求m的值.
m=12和m=24
试题分析:方程有整数根,则根的判别式就为完全平方数,所以就是求使△为完全平方数的m的值,求得后再代入方程检验即可.
∵a=1,b=-2(2m-3),c=4m2-14m+8,
∴△=b2-4ac=4(2m-3)2-4(4m2-14m+8)=4(2m+1).
∵方程有两个整数根,
∴△=4(2m+1)是一个完全平方数,
所以2m+1也是一个完全平方数.
∵4<m<40,
∴9<2m+1<81,
∴2m+1=16,25,36,49或64,
∵m为整数,
∴m=12或24.
代入已知方程,
得x=16,26或x=38,52.
综上所述m为12,或24.
点评:一元二次方程有整数根,必须满足根的判别式△=b2-4ac非负或为完全平方数,可根据这两个条件来限定待定系数的取值范围,从而找出解题的思路.

练习册系列答案
相关题目
 的速度移动,与此同时,点Q从点B开始沿边BC向点C以
的速度移动,与此同时,点Q从点B开始沿边BC向点C以 的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,问:
的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,问: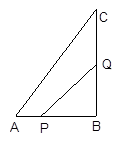
 的面积等于
的面积等于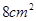 ?
? +b)2=
+b)2= )2-(
)2-( )2, 这个公式形似平方差公式,我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。
)2, 这个公式形似平方差公式,我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。 +
+ -
-
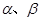 是一元二次方程
是一元二次方程 的两个根,那么
的两个根,那么 的值是_______。
的值是_______。 的两个实数根之积为
的两个实数根之积为 .你认为正确的共有( )
.你认为正确的共有( ) (2)
(2)