题目内容
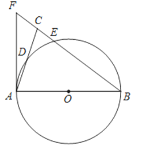
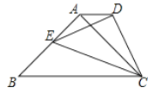
【题目】如图①,在△ABC中,AB=AC,∠BAC=60°,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转60°得到AE,连接EC,则:
(1)①∠ACE的度数是 ; ②线段AC,CD,CE之间的数量关系是 .
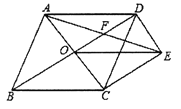
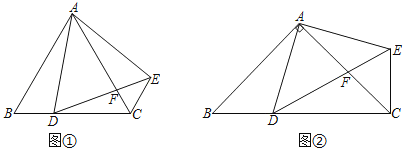
(2)如图②,在△ABC中,AB=AC,∠BAC=90°,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,请判断线段AC,CD,CE之间的数量关系,并说明理由;
(3)如图②,AC与DE交于点F,在(2)条件下,若AC=8,求AF的最小值.
【答案】(1)60°,AC=CE+CD;(2)![]() =CE+CD,见详解;(3)4.
=CE+CD,见详解;(3)4.
【解析】
(1)①先判断出∠BAD=∠CAE,即可判断出△ABD≌△ACE,即可得出结论;
②由①得,△ABD≌△ACE,得出BD=CE,即可得出结论;
(2)先判断出BC=![]() AC,再同(1)的方法判断出△ABD≌△ACE,即可得出结论;
AC,再同(1)的方法判断出△ABD≌△ACE,即可得出结论;
(3)先判断出点A,D,C,E四点共圆,再由AF最小判断出四边形ADCE是矩形,即可得出结论.
解:(1)①∵△ABC是等边三角形,
∴AB=AC,∠B=∠BAC=60°,
由旋转知,AD=AE,∠DAE=60°=∠BAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠B=60°,
故答案为60°;
②由(1)知,△ABD≌△ACE,
∴BD=CE,
∴BC=BD+CD=CE+CD,
∵△ABC是等边三角形,
∴AC=BC,
∴AC=CE+CD,
故答案为AC=CE+CD;
(2)在△ABC中,AB=AC,∠BAC=90°,
∴BC=![]() ,
,
由旋转知,AD=AE,∠DAE=90°=∠BAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD+CD=CE+CD,
∴![]() =CE+CD;
=CE+CD;
(3)由(2)知,△ABD≌△ACE,
∴ACE=∠ABD,
在△ABC中,AB=AC,∠BAC=90°,
∴∠ABD=∠ACB=45°,
∴∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=90°,
∵∠DAE=90°,
∴∠BCE+∠DAE=180°,
∴点A,D,C,E在以DE为直径的圆上,
∵AC与DE交于点F,
∴AF是直径DE上的一点到点A的距离,
即:当AF⊥DE时,AF最小,
∴∠CFD=90°,
∴∠CDF=90°﹣∠ACB=45°,
∵∠ADE=45°,
∴∠ADC=90°,
∴四边形ADCE是矩形,
∴AF最小=![]() AC=4.
AC=4.