题目内容
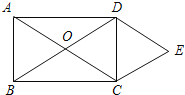
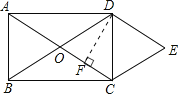
【题目】如图,矩形![]() 的对角线相交于点
的对角线相交于点![]() ,
,![]() ,
,![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,菱形
,菱形![]() 的面积为
的面积为![]() ,求
,求![]() 的长.
的长.
【答案】![]()
【解析】
(1)首先根据两对边互相平行的四边形是平行四边形证明四边形OCED是平行四边形,再根据矩形的性质可得OC=OD,即可利用一组邻边相等的平行四边形是菱形判定出结论;
(2)因为∠BAC=60°,可得∠ACB=30°可证明菱形的一条对角线和边长相等,可证明和对角线构成等边三角形,然后过点D作DF⊥AC于F,根据菱形的面积求出OC,再利用勾股定理求出BC.
解:(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AO=OC=BO=OD,
∴四边形OCED是菱形;
(2)∵∠BAC=60°,
∴∠ACB=30°,
∴∠DCO=90°-30°=60°,
又∵OD=OC,
∴△OCD是等边三角形,
又∵菱形OCED的面积═△OCD的面积的2倍=18![]() ,
,
过点D作DF⊥AC于F,
可得2CF=OC=CD,
∴DF=![]() CD=
CD=![]() OC,
OC,
∴即18![]() =OC×DF=OC×
=OC×DF=OC×![]() OC=
OC=![]() OC2,
OC2,
∴OC2=36,
∴OC=6=CD,
∴BD=2CD=2OC=12,
∴BC=![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】勤俭节约一直是中华民族的传统美德,某中学校团委准备以“勤俭节约”为主题开展一次演讲比赛,为此先对同学们每月零花钱的数额进行一些了解,随机调查了本校部分同学,根据调查结果绘制出了如下两个尚不完整的统计图表.
组别 | 分组(单位:元) | 人数 |
|
| 4 |
|
|
|
|
|
|
|
| 8 |
|
| 2 |
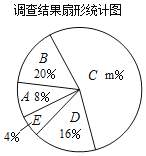
根据统计图表中的信息,解答下列问题:
(1)![]() ,
,![]() ,
,![]() ;
;
(2)扇形统计图中扇形![]() 的圆心角的度数为
的圆心角的度数为 ![]() ;所抽取同学零花钱的数额的中位数落在 范围;
;所抽取同学零花钱的数额的中位数落在 范围;
(3)该校共有1200名学生,请估计每月零花钱的数额在![]() 范围的人数.
范围的人数.