Question

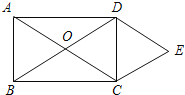
【题目】如图1，在四边形ABCD中，∠BAD＝∠BDC＝90°，AB＝AD，∠DCB＝60°，CD＝8．

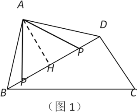
（1）若P是BD上一点，且PA＝CD，求∠PAB的度数．

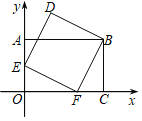
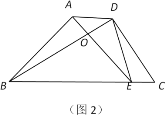
（2）①将图1中的△ABD绕点B顺时针旋转30°，点D落在边BC上的E处，AE交BD于点O，连接DE，如图2，求证：DE2＝DODB；

②将图1中△ABD绕点B旋转α得到△A'BD'(A与A'，D与D'是对应点)，若CD'＝CD，则cosα的值为 ．

Answer 1

【答案】（1）∠P'AB＝75°或15°（2）①见解析②

【解析】

（1）先解直角三角形BDC与直角三角形ABD，过点H作AH⊥BD于H，分点P在点H的左侧和右侧两种情况，分别解直角三角形即可；

（2）

①利用旋转的性质求出∠AEB=45°，∠DOE=∠DEB=75°，证△BDE∽△EDO即可；

②根据题意△ABD绕点B旋转α得到△A'BD'(A与A'，D与D'是对应点)，CD'＝CD，则cosα的值为.

（1）在Rt△BDC中，∠DCB＝60°，CD＝8，

∴ BC＝16，BD＝8，

在Rt△ABD中，AB＝AD，

∴ ∠ABD＝∠ADB＝45°，

∴ AB＝AD＝8× ＝4 ，

如图1，过点H作AH⊥BD于H，

则∠BAH＝∠DAH＝45°，AH＝ BD＝4，

当点P在点H右侧时，

在Rt△AHP中，AH＝4，AP＝DC＝8，∴ ∠HAP＝30°，

∴ ∠PAB＝∠BAH＋∠HAP＝75°．

当点P'在点H左侧时，

∴ ∠P'AB＝∠BAH－∠HAP'＝15°．

综上所述，∠P'AB＝75°或15°．

（2）①由题意知，BE与BC在同一条直线上，∠AEB＝45°，BD＝BE，

∵ ∠DBE＝30°，

∴ ∠BDE＝∠BED＝ (180°－30°)＝75°，∠DOE＝∠DBE＋∠AEB＝75°，

∵ ∠BDE＝∠EDO，∠DOE＝∠DEB＝75°，

∴△BDE∽△EDO，

∴ ，

∴ DE2＝DODB．

（3）根据题意△ABD绕点B旋转α得到△A'BD'(A与A，D与D'是对应点)，CD'＝CD，则cosα的值为.