��Ŀ����
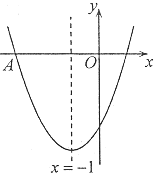
����Ŀ����ͼ����![]() �У�
��![]() =5��
=5��![]() =9��
=9��![]() =
=![]() ������
������![]() ��
��![]() ������������
������������![]() ������ÿ��5����λ���ȵ��ٶ��˶�������
������ÿ��5����λ���ȵ��ٶ��˶�������![]() ��
��![]() �������һ��ͬ���ٶ����߶�
�������һ��ͬ���ٶ����߶�![]() ����
����![]() ��
��![]() �˶�����
�˶�����![]() ���˶���
���˶���![]() ��ʱ��
��ʱ��![]() ����ͬʱֹͣ�˶�����
����ͬʱֹͣ�˶�����![]() Ϊ����������
����������![]() (
(![]() ����ʱ������)����
����ʱ������)����![]() Ϊ����
Ϊ����![]() �Ϸ���������
�Ϸ���������![]() .
.
(1)![]() _______.
_______.
(2)���![]() �˶�ʱ��Ϊ
�˶�ʱ��Ϊ![]() ��������
��������![]() �����Ϊ
�����Ϊ![]() ,��̽��
,��̽��![]() �Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵������.
�Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵������.
(3)��![]() Ϊ��ֵʱ��������
Ϊ��ֵʱ��������![]() ��ij������(
��ij������(![]() �����)����������
�����)����������![]() �ı�
�ı�![]() �ϣ���ֱ��д��
�ϣ���ֱ��д��![]() ��ֵ.
��ֵ.
���𰸡�(1)![]() ��(2)���ڣ�
��(2)���ڣ�![]() ��(3)
��(3)![]() ��
��![]() .
.
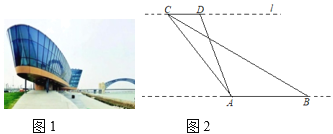
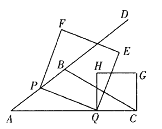
��������
(1)����B��BM��AC�ڵ�M.���������ε������ʽ�����![]() .�ɹ��ɶ�����
.�ɹ��ɶ�����![]() ���Ӷ��õ�
���Ӷ��õ�![]() .
.
(2)����.����![]() ��
��![]() �ڵ�N.������ɵ�
�ڵ�N.������ɵ�![]() ,��Ϊ
,��Ϊ![]() ����
����![]() .�õ�
.�õ�![]() .���ݹ��ɶ�����
.���ݹ��ɶ�����![]() ,��
,��
![]() ���ٸ��ݶ��κ��������ʽ�����⼴�ɵõ���.
���ٸ��ݶ��κ��������ʽ�����⼴�ɵõ���.
�⣺(1)����B��BM��AC�ڵ�M.
![]() ��
��
![]() ����
����![]() ��
��
���![]() .
.
�ɹ��ɶ�������![]() ��
��
��![]() .
.
(2)����.
����![]() ��
��![]() �ڵ�N.�������
�ڵ�N.�������![]() ,
,
![]() ��
��
![]() .
.
![]() .
.
���ݹ��ɶ�����![]() ,
,
![]() (
(![]() ).
).
![]() ,
,![]() .
.
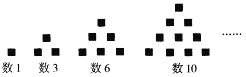
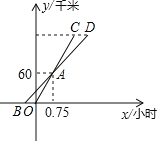
����ͼ1������![]() �ڱ�
�ڱ�![]() ��ʱ��
��ʱ��![]() ��
��
����ͼ2������![]() �ڱ�
�ڱ�![]() ��ʱ��
��ʱ��![]() .
.


��ϰ��ϵ�д�
 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
�����Ŀ