题目内容
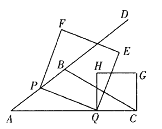
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点且AE=BF,连接CE、AF交于点H,连接DH交AG于点O,则下列结论①△ABF≌△CAE;②∠AHC=120°;③AE+CH>CD,中正确的是____.

【答案】①②③
【解析】
由菱形的性质得出CD=AB=BC,由AB=AC,推出AB=BC=AC,即△ABC是等边三角形,同理可得△ADC是等边三角形,则∠B=∠EAC=60°,由SAS即可证得△ABF≌△CAE;得出∠BAF=∠ACE,由外角性质得出∠AEH=∠B+∠BCE,由外角性质得出∠AHC=∠BAF+∠AEH即可得出结果;由△ABF≌△CAE得出AE=BF,由∠AHC=120°得出∠CHF=60°,由△ABC是等边三角形得出∠ACB=60°,则∠HCF<60°,推出∠HFC>60°,则∠HFC>∠CHF得出CH>FC,即可得出结果.
∵四边形ABCD是菱形,
∴CD=AB=BC,
∵AB=AC,
∴AB=BC=AC,
即△ABC是等边三角形,
同理:△ADC是等边三角形,
∴∠B=∠EAC=60°,
在△ABF和△CAE中,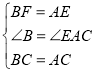 ,
,
∴△ABF≌△CAE(SAS);
故①正确;
∴∠BAF=∠ACE,
∵∠AEH=∠B+∠BCE,
∴∠AHC=∠BAF+∠AEH=∠BAF+∠B+∠BCE=∠B+∠ACE+∠BCE=∠B+∠ACB=60°+60°=120°;
故②正确;
∵△ABF≌△CAE,
∴AE=BF,
∵∠AHC=120°,
∴∠CHF=60°,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠HCF<60°,
∴∠HFC>60°,
∴∠HFC>∠CHF,
∴CH>FC,
∵CD=BC=BF+FC=AE+FC,
∴AE+CH>AE+FC,
即AE+CH>CD;
故③正确;
故答案为①②③.