题目内容
【题目】正三角形外接圆面积是
，其内切圆面积是（ ）
A.
B.
C.
D.
【答案】D
【解析】
△ABC为等边三角形，利用外接圆和内切圆的性质得∠OBC=30°，在Rt△OBD中，利用含30°的直角三角形三边的关系得到OD=
OB，然后根据圆的面积公式得到△ABC的外接圆的面积与其内切圆的面积之比，即可得解.
△ABC为等边三角形，AD为角平分线，⊙O为△ABC的内切圆，连OB，如图所示：
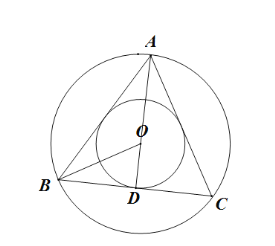
∵△ABC为等边三角形，⊙O为△ABC的内切圆，
∴点O为△ABC的外心，AD⊥BC，
∴∠OBC=30°，
在Rt△OBD中，OD=OB，
∴△ABC的外接圆的面积与其内切圆的面积之比=OB2：OD2=4：1．
∵正三角形外接圆面积是
，
∴其内切圆面积是
故选：D.
练习册系列答案
名校课堂系列答案
相关题目
