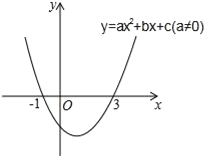题目内容
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)观察猜想:如图(1),当点D在线段BC上时,
①BC与CF的位置关系是: ;
②BC、CD、CF之间的数量关系为: (将结论直接写在横线上)
(2)数学思考:如图(2),当点D在线段CB的延长线上时,上述①、②中的结论是否仍然成立?若成立,请给予证明,若不成立,请你写出正确结论再给予证明.

【答案】(1)①BC⊥CF;②BC=CF+CD;(2)CF⊥BC成立;BC=CD+CF不成立,CD=CF+BC.证明见解析.
【解析】试题分析:(1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论;
②由正方形ADEF的性质可推出△DAB≌△FAC,根据全等三角形的性质得到CF=BD,∠ACF=∠ABD,根据余角的性质即可得到结论;
(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论.
试题解析:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中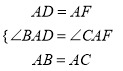 ,∴△DAB≌△FAC,
,∴△DAB≌△FAC,
∴∠B=∠ACF,∴∠ACB+∠ACF=90°,即BC⊥CF;
故答案为:BC⊥CF;
②△DAB≌△FAC,∴CF=BD,
∵BC=BD+CD,∴BC=CF+CD;
故答案为:BC=CF+CD;
(2)CF⊥BC成立;BC=CD+CF不成立,CD=CF+BC.
∵正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中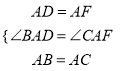 ,∴△DAB≌△FAC,∴∠ABD=∠ACF,
,∴△DAB≌△FAC,∴∠ABD=∠ACF,
∵∠BAC=90°,AB=AC,∴∠ACB=∠ABC=45°.∴∠ABD=180°﹣45°=135°,
∴∠BCF=∠ACF﹣∠ACB=135°﹣45°=90°,∴CF⊥BC.
∵CD=DB+BC,DB=CF,∴CD=CF+BC.

【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:则 a=___.
学生最喜爱的节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |