题目内容
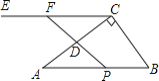
【题目】如图，在△ABC中，∠BAC＝90°，AB＝AC，点D、点E分别在AB、BC边上，若∠BED+
∠AED＝45°，过点D作DF⊥BC，垂足为F，若BC＝3
，则EF＝_____．
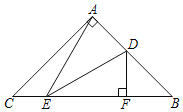
【答案】
【解析】
如图中，作EH⊥AB于H，DG⊥AB交BC于点G．只要证明AE=DE，BF=FG，GE=EC即可解决问题．
解：如图中，作EH⊥AB于H，DG⊥AB交BC于点G．
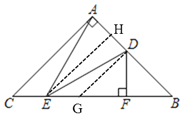
∵AB=AC，∠BAC=90°，
∴∠B=∠C=45°，
∵EH⊥AB，
∴∠EHB=90°，
∴∠BEH=45°，
∴∠BED+∠DEH=45°，
∵2∠BED+∠AED=90°，
∴∠BED+∠AEH=45°，
∴∠DEH=∠AEH，
∵∠EDH+∠DEH=90°，∠EAH+∠HEA=90°，
∴∠EDH=∠EAH，
∴ED=EA．
∵∠B=45°，∠BDG=90°，
∴∠B=∠BGD=45°，
∴DB=DG，
∵DF⊥BG，
∴BF=FG，
∵ED=EA，EH⊥AD，
∴DH=HA，
∵DG∥EH∥AC，
∴EG=EC，
∴EF=FG+GE=
BG+CG=BC=．
答案为：．
练习册系列答案
相关题目
