题目内容
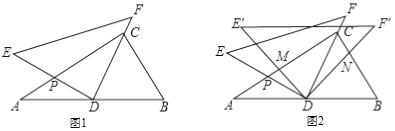
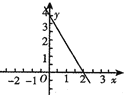
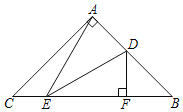
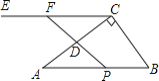
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,
中点,![]() ,动点
,动点![]() 以每秒1个单位长的速度从点
以每秒1个单位长的速度从点![]() 出发向点
出发向点![]() 移动,连接
移动,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,设点
,设点![]() 移动时间为
移动时间为![]() 秒.
秒.
(1)求![]() 与
与![]() 间的距离;
间的距离;
(2)![]() 为何值时,四边形
为何值时,四边形![]() 为平行四边形;
为平行四边形;
(3)当PF=4时,求t的值
【答案】(1)2.4;(2)2.5;(3)1.8;
【解析】
(1)根据勾股定理,可得AB的长,根据面积的不同表示方法,可得答案;
(2)根据两组对边分别平行的四边形是平行四边形,可得答案;
(3)根据已知条件判定△CDF≌△ADP,即可得出AP=CF,进而得到四边形APCF为平行四边形,依据AC=PF,即可得到四边形APCF为矩形.再根据勾股定理即可得到PB的长,进而得出t=1.8.
(1)在Rt△ABC中,AB=5,BC=3,
∴AC=![]() =4.
=4.
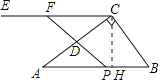
如图,过C作CH⊥AB于H,则由![]() ABCH=
ABCH=![]() ACBC,
ACBC,
得CH=![]() =2.4.
=2.4.
∵CE∥AB,
∴AB与CE之间的距离为2.4.
(2)∵CE∥AB,
∴当PF∥BC时,四边形PBCF是平行四边形.
∵D为AC的中点,
∴P为AB的中点.
∴t=PB=![]() AB=2.5.
AB=2.5.
(3)∵CE∥AB,
∴∠DCF=∠DAP,∠DFC=∠DPA.
∵D为AC的中点,
∴CD=AD,
∴△CDF≌△ADP(AAS).
∴AP=CF,
∴四边形APCF为平行四边形.
∵AC=4,PF=4.
∴AC=PF.
∴四边形APCF为矩形.
∴CP⊥AB.
在Rt△CPB中,CP=2.4,BC=3,
∴PB=![]() =1.8.
=1.8.
∴t=1.8.

练习册系列答案
相关题目