题目内容
【题目】如图,有一座石拱桥的桥拱是以![]() 为圆心,
为圆心,![]() 为半径的一段圆弧.
为半径的一段圆弧.

![]() 请你确定弧
请你确定弧![]() 的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
![]() 如果已知石拱桥的桥拱的跨度(即弧所对的弦长)为
如果已知石拱桥的桥拱的跨度(即弧所对的弦长)为![]() 米,拱高(即弧的中点到弦的距离)为
米,拱高(即弧的中点到弦的距离)为![]() 米,求桥拱所在圆的半径.
米,求桥拱所在圆的半径.
【答案】(1)详见解析;(2)桥拱所在圆的半径为![]() .
.
【解析】
(1)根据垂径定理可以作弦AB的垂直平分线,和弧的交点即是弧的中点;
(2)设圆O的半径为r,在Rt△ADO中由勾股定理列出方程求出r即可.
(1)如图:点E即为所求的中点;
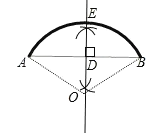
(2)过圆O作OE⊥AB于D,在直角三角形AOD中,AB=24m,DE=8m,
∴AD=![]() AB=12(cm),
AB=12(cm),
设AO=rcm,
∴OD=r8(cm),
∴r2=122+(r8)2
解得:r=13cm.
答:桥拱所在圆的半径为13cm.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目